
 时,求抛物线的解析式;
时,求抛物线的解析式; ,a2+(2a)2=20,
,a2+(2a)2=20, 或
或 (6分)
(6分) 或
或 (不合题意,舍去)
(不合题意,舍去)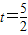 或
或 .(7分)
.(7分)

 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源:2010年北京市中考模拟试卷汇总:圆(解析版) 题型:解答题
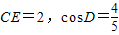 ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源:2011年浙江省杭州市中考数学模拟试卷(38)(解析版) 题型:选择题
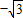 ,1),点B是x轴上的一动点,以AB为边作等边三角形ABC、当C(x,y)在第一象限内时,下列图象中,可以表示y与x的函数关系的是( )
,1),点B是x轴上的一动点,以AB为边作等边三角形ABC、当C(x,y)在第一象限内时,下列图象中,可以表示y与x的函数关系的是( )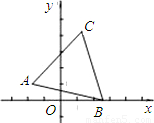




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com