【题目】如图，点P是∠AOB的边OB上的一点．
（1）过点P画OB的垂线，交OA于点C；
（2）过点P画OA的垂线，垂足为H；
（3）线段PH的长度是点P到______的距离，______是点C到直线OB的距离，线段PC、PH、OC这三条线段大小关系是______（用“＜”号连接）．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，一次函数y=kx+b（k，b都是常数，且k≠0）的图象经过点（1，0）和（0，2）．
（1）当﹣2＜x≤3时，求y的取值范围；
（2）已知点P（m，n）在该函数的图象上，且m﹣n=4，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图，其对称轴为直线x=﹣1，给出下列结果：（1）b2＞4ac；（2）abc＞0；（3）2a+b=0；（4）a+b+c＞0；（5）a﹣b+c＜0．
则正确的结论是（ ）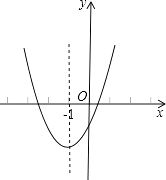
A.（1）（2）（3）（4）
B.（2）（4）（5）
C.（2）（3）（4）
D.（1）（4）（5）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
，点
在
上，以
为半径的
交
于点
，
的垂直平分线交
于点
，交于点
，连接
．
（1）判断直线与的位置关系，并说明理由；
（2）若
，
，
，求线段的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题探究
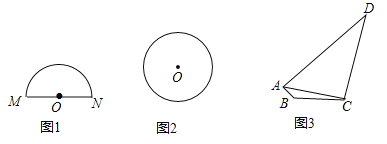
（1）如图1，请在半径为
的半圆
内（含弧和直径
）画出面积最大的三角形，并求出这个三角形的面积；
（2）如图2，请在半径为的
内（含弧）画出面积最大的矩形
，并求出这个矩形的面积；
问题解决
（3）如图3，
是一块草坪，其中
，
，
，某开发商现准备再征一块地，把扩充为四边形，使
，是否存在面积最大的四边形？若存在，求出四边形的最大面积；若不存在，请说明理由．（结果保留根号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用A4纸复印文件，在甲复印店不管一次复印多少页，每页收费0.1元．在乙复印店复印同样的文件，一次复印页数不超过20时，每页收费0.12元；一次复印页数超过20时，超过部分每页收费0.09元．
设在同一家复印店一次复印文件的页数为x(x为非负整数)．
(1)根据题意，填写下表：
一次复印页数(页) | 5 | 10 | 20 | 30 | … |
甲复印店收费(元) | 0.5 |
| 2 |
| … |
乙复印店收费(元) | 0.6 |
| 2.4 |
| … |
(2)设在甲复印店复印收费y1元，在乙复印店复印收费y2元，分别写出y1，y2关于x的函数关系式；
(3)当x＞70时，顾客在哪家复印店复印花费少？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】规定两数a，b之间的一种运算，记作(a，b)：如果
，那么(a，b)=c．
例如：因为23=8，所以(2，8)=3．
（1）根据上述规定，填空：
（3，27）=_______，（5，1）=_______，（2，
）=_______．
（2）小明在研究这种运算时发现一个现象：（3n，4n）=（3，4）小明给出了如下的证明：
设（3n，4n）=x，则（3n）x=4n，即（3x）n=4n
所以3x=4，即（3，4）=x，
所以（3n，4n）=（3，4）．
请你尝试运用这种方法证明下面这个等式：(3，4)+(3，5)=(3，20)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现计划把一批货物用一列火车运往某地
已知这列火车可挂A，B两种不同规格的货车厢共40节，使用A型车厢每节费用6000元，使用B型车厢每节费用为8000元．
设运送这批货物的总费用为y元，这列火车挂A型车厢x节，写出y关于x的函数表达式，并求出自变量x的取值范围；
已知A型车厢数不少于B型车厢数，运输总费用不低于276000元，问有哪些不同运送方案？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
