
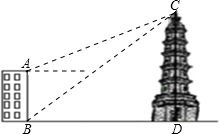
 如图,大楼AB高16m,远处有一塔CD,某人在楼底B处测得塔顶C的仰角为39°,在楼顶A处测得塔顶的仰角为22°,求塔高CD的高.(结果保留小数后一位)
如图,大楼AB高16m,远处有一塔CD,某人在楼底B处测得塔顶C的仰角为39°,在楼顶A处测得塔顶的仰角为22°,求塔高CD的高.(结果保留小数后一位)分析 过点A作AE⊥CD于点E,由题意可知:∠CAE=22°,∠CBD=39°,ED=AB=16米,设大楼与塔之间的距离BD的长为x米,则AE=BD=x,分别在Rt△BCD中和Rt△ACE中,用x表示出CD和CE=AE,利用CD-CE=DE得到有关x的方程,求得x的值即可.
解答 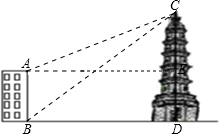 解:过点A作AE⊥CD于点E,
解:过点A作AE⊥CD于点E,
由题意可知:∠CAE=22°,∠CBD=39°,ED=AB=16米
设大楼与塔之间的距离BD的长为x米,则AE=BD=x米,
∵在Rt△BCD中,tan∠CBD=$\frac{CD}{BD}$,
∴CD=BD tan 39°≈0.81x,
∵在Rt△ACE中,tan∠CAE=$\frac{CE}{AE}$,
∴CE=AE×tan 22°≈0.4x,
∵CD-CE=DE,
∴0.81x-0.4x=16,
解得x≈39.0,
即BD=39.0(米),
∴CD=0.81×39.0=31.6(米),
答:塔高CD是31.6米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,解答此题的关键是作出辅助线,构造出直角三角形,利用直角三角形的性质进行解答.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5×102吨 | B. | 5×106吨 | C. | 5×107吨 | D. | 5×108吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)2=a2+b2 | B. | (2a2)3=6a6 | C. | a3•a2=a6 | D. | $\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+3a2=3a3 | B. | (a-b)2=a2-ab+b2 | C. | 2(a-b)=2a-2b | D. | (2ab)2÷ab=2ab |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四边都相等的四边形是矩形 | |
| B. | 菱形的对角线相等 | |
| C. | 对角线互相垂直的平行四边形是正方形 | |
| D. | 对角线相等的平行四边形是矩形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com