

分析 (1)由小麦先摸到了“仕”,“仕”胜“相”、“兵”;可得这一轮中小麦胜小辉的有7种情况,然后利用概率公式求解即可求得答案;
(2)分别求得摸到“相”、“仕”;“兵”“帅”胜的概率即可.
解答 解:(1)∵小麦先摸到了“仕”,“仕”胜“相”、“兵”;
∴这一轮中小麦胜小辉的有5种情况,
∴这一轮中小麦胜小辉的概率为:$\frac{5}{7}$;
(3)①摸到“相”胜的概率为:$\frac{3}{7}$;
②摸到“仕”胜的概率为:$\frac{5}{7}$,
③摸到“帅”胜的概率为:$\frac{4}{7}$,
④摸到“兵”胜的概率为:$\frac{1}{7}$.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
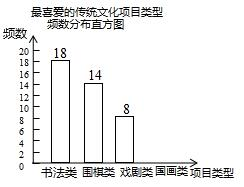 某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.| 项目类型 | 频数 | 频率 |
| 书法类 | 18 | a |
| 围棋类 | 14 | 0.28 |
| 喜剧类 | 8 | 0.16 |
| 国画类 | b | 0.20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
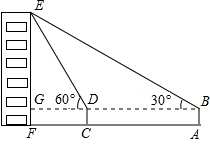 如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.($\sqrt{3}$=1.732,结果精确到0.1米)
如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.($\sqrt{3}$=1.732,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
| 学生人数(人) | 1 | 3 | 2 | 2 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
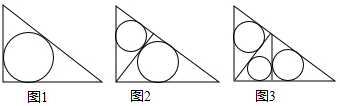
| A. | π | B. | $\sqrt{2}$π | C. | 1.6π | D. | $\frac{3}{2}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,大楼AB高16m,远处有一塔CD,某人在楼底B处测得塔顶C的仰角为39°,在楼顶A处测得塔顶的仰角为22°,求塔高CD的高.(结果保留小数后一位)
如图,大楼AB高16m,远处有一塔CD,某人在楼底B处测得塔顶C的仰角为39°,在楼顶A处测得塔顶的仰角为22°,求塔高CD的高.(结果保留小数后一位)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com