
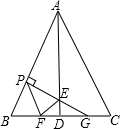
 ��ͼ���ڱ߳�Ϊ2�ĵȱߡ�ABC�У�AD��BC����PΪ��AB ��һ�����㣬��P����PF��AC���߶�BD�ڵ�F����PG��AB��AD�ڵ�E�����߶�CD�ڵ�G����BP=x��
��ͼ���ڱ߳�Ϊ2�ĵȱߡ�ABC�У�AD��BC����PΪ��AB ��һ�����㣬��P����PF��AC���߶�BD�ڵ�F����PG��AB��AD�ڵ�E�����߶�CD�ڵ�G����BP=x��| 1 |
| 2 |
| ED |
| BP |
| DG |
| PG |
| BP |
| AB |
| BF |
| BC |
| DE |
| AD |
| DF |
| BD |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| BG2-BP2 |
| 3 |
| ED |
| BP |
| DG |
| PG |
| DE |
| x |
| 2x-1 | ||
|
2
| ||
| 3 |
| ||
| 3 |
| BP |
| AB |
| BF |
| BC |
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 2 |
| ||
| 6 |
| ||
| 3 |
| 3 |
| 4 |
| ||
| 48 |
| ||
| 48 |
| ||
| 3 |
| ||
| 2 |
| ||
| 6 |
| ||
| 48 |
| DE |
| AD |
| DF |
| BD |
| ||||||||
|
| 1-x |
| 1 |
| 4 |
| 5 |
| 2 |
| 3 |
| 4 |
| 5 |
| 2 |
| 3 |
| 4 |
| 5 |
| 2 |
| 3 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ���ڱ߳�Ϊ1�ĵȱ�������ABC�У�����������120��Բ�Ľǵ�
��ͼ���ڱ߳�Ϊ1�ĵȱ�������ABC�У�����������120��Բ�Ľǵ� |
| AOB |
 |
| BOC |
A��
| ||
B��
| ||
C��
| ||
D��
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ���ڱ߳�Ϊ4�ĵȱ�������ABC�У�AD��BC���ϵĸߣ���E��F��AD�ϵ����㣬��ͼ����Ӱ���ֵ�����ǣ�������
��ͼ���ڱ߳�Ϊ4�ĵȱ�������ABC�У�AD��BC���ϵĸߣ���E��F��AD�ϵ����㣬��ͼ����Ӱ���ֵ�����ǣ�������A��4
| ||
B��3
| ||
C��2
| ||
D��
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ���ڱ߳�Ϊ20cm�ĵȱ�������ABCֽƬ�У��Զ���CΪԲ�ģ��Դ������εĸ�Ϊ�뾶�����ֱ�AC��BC�ڵ�D��E��������CDE��Χ��Բ�����ƽӷ죩�ĵ�Բ�뾶Ϊ��������
��ͼ���ڱ߳�Ϊ20cm�ĵȱ�������ABCֽƬ�У��Զ���CΪԲ�ģ��Դ������εĸ�Ϊ�뾶�����ֱ�AC��BC�ڵ�D��E��������CDE��Χ��Բ�����ƽӷ죩�ĵ�Բ�뾶Ϊ��������A��
| ||||
B��
| ||||
C��5
| ||||
D��10
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��AD�ڵ�E�����߶�CD�ڵ�G����BP=x��
��AD�ڵ�E�����߶�CD�ڵ�G����BP=x���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•�人ģ�⣩��ͼ���ڱ߳�Ϊ1�ĵȱߡ�OAB�У��Ա�ABΪֱ������D����OΪԲ��OA��Ϊ�뾶��ԲO��CΪ��ԲAB�ϲ���A��B�غϵ�һ���㣬����AC����O�ڵ�E��BC=a��AC=b��
��2013•�人ģ�⣩��ͼ���ڱ߳�Ϊ1�ĵȱߡ�OAB�У��Ա�ABΪֱ������D����OΪԲ��OA��Ϊ�뾶��ԲO��CΪ��ԲAB�ϲ���A��B�غϵ�һ���㣬����AC����O�ڵ�E��BC=a��AC=b��| 3 |
| 3 |
| 3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com