
【题目】如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交 ![]() 于点F,交过点C的切线于点D.
于点F,交过点C的切线于点D. 
(1)求证:DC=DP;
(2)若直径AB=12cm,∠CAB=30°, ①当E是半径OA中点时,切线长DC=cm:
②当AE=cm时,以A,O,C,F为顶点的四边形是菱形.
【答案】
(1)证明:连接OC.
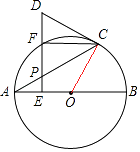
∵CD是⊙O的切线,
∴∠OCD=90°,
∵OA=OC,
∴∠OAC=∠OCA,
∵PE⊥AB,
∴∠PEA=90°,
∴∠OAC+∠APE=90°,∠OCA+∠PCD=90°,
∴∠APE=∠PCD,
∵∠APE=∠CPD,
∴∠PCD=∠CPD,
∴DC=DP.
(2)4 ![]() ;3
;3
【解析】解:(2)①连接BC, 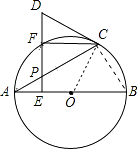
∵AB是直径,
∴∠ACB=90°
∵∠A=30°,AB=12,
∵AC=ABcos30°=6 ![]() ,
,
在Rt△APE中,∵AE= ![]() OA=3,
OA=3,
∴AP=AE÷cos30°=2 ![]() ,
,
∴PC=AC﹣AP=4 ![]() ,
,
∵∠APE=∠DPC=60°,DP=DC,
∴△DPC是等边三角形,
∴DC=4 ![]() ,
,
所以答案是4 ![]()
. ②当AE=EO时,四边形AOCF是菱形.
理由:连接AF、OF.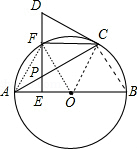
∵AE=EO,FE⊥OA,
∴FA=FO=OA,
∴△AFO是等边三角形,
∴∠FAO=60°,∵∠CAB=30°,
∴∠FAC=30°,∠FOC=2∠FAC=60°,
∴△FOC是等边三角形,
∴CF=CO=OA=AF,
∴四边形AOCF是菱形,
∴AE=3cm时,四边形AECF是菱形.
所以答案是3.
【考点精析】本题主要考查了菱形的判定方法和垂径定理的相关知识点,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】万美服装店准备购进一批两种不同型号的衣服,已知若购进A型号的衣服9件,B型号的衣服10件共需1 810元;若购进A型号的衣服12件,B型号的衣服8件共需1 880元.已知销售一件A型号的衣服可获利18元,销售一件B型号的衣服可获利30元.
(1)求A、B型号衣服的进价各是多少元?
(2)若已知购进的A型号的衣服比B型号衣服的2倍还多4件,且购进的A型号的衣服不多于28件,则该服装店要想获得的利润不少于699元,在这次进货时可有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是 . 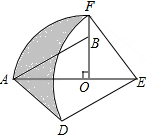
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )

A. 110° B. 120° C. 130° D. 140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.

(1)求证:AD垂直平分EF;
(2)若∠BAC=60°,猜测DG与AG间有何数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一单位长度为1cm的方格纸上,依如图所示的规律,设定点A1、A2、A3、A4、A5、A6、A7、…、An,连接点O、A1、A2组成三角形,记为△1,连接O、A2、A3组成三角形,记为△2…,连O、An、An+1组成三角形,记为△n(n为正整数),请你推断,当n为50时,△n的面积=( )cm2.

A. 1275 B. 2500 C. 1225 D. 1250
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1 , 0),(x2 , 0),且x1<x2 , 图象上有一点M(x0 , y0)在x轴下方,对于以下说法: ①b2﹣4ac>0;
②x=x0是方程ax2+bx+c=y0的解;
③x1<x0<x2
④a(x0﹣x1)(x0﹣x2)<0;
⑤x0<x1或x0>x2 ,
其中正确的有( )
A.①②
B.①②④
C.①②⑤
D.①②④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com