
 如图,已知△ABC中,AB>AC,BC=6,BC边上的高AN=4.直角梯形DEFG的底EF在BC边上,EF=4,点D、G分别在边AB、AC上,且DG∥EF,GF⊥EF,垂足为F.设GF的长为x,直角梯形DEFG的面积为y,求y关于x的函数关系式,并写出函数的定义域.
如图,已知△ABC中,AB>AC,BC=6,BC边上的高AN=4.直角梯形DEFG的底EF在BC边上,EF=4,点D、G分别在边AB、AC上,且DG∥EF,GF⊥EF,垂足为F.设GF的长为x,直角梯形DEFG的面积为y,求y关于x的函数关系式,并写出函数的定义域. 分析 由平行线分线段成比例定理得出$\frac{DG}{BC}$=$\frac{AG}{AC}$,证出四边形GFMN为矩形,得出GF=MN=x,由平行线分线段成比例定理得出$\frac{AG}{AC}$=$\frac{AM}{AN}$,得出$\frac{DG}{6}$=$\frac{4-x}{4}$,因此DG=6-$\frac{3}{2}$x,即可得出结果.
解答 解:∵DG∥EF,
∴DG∥BC,
∴$\frac{DG}{BC}$=$\frac{AG}{AC}$,
∵GF⊥EF,AN⊥BC,四边形DEFG为直角梯形,
∴四边形GFMN为矩形,
∴GF=MN=x,
∵DG∥BC,
∴$\frac{AG}{AC}$=$\frac{AM}{AN}$=$\frac{AN-GF}{AN}$=$\frac{4-x}{4}$,
∴$\frac{DG}{BC}$=$\frac{4-x}{4}$,
即:$\frac{DG}{6}$=$\frac{4-x}{4}$,
解得:DG=6-$\frac{3}{2}$x,
∴y=$\frac{(DG+EF)}{2}$•MN=$\frac{(6-\frac{3}{2}x+4)}{2}$•x=-$\frac{3}{4}$x2+5x,
即y关于x的函数关系式为:y═-$\frac{3}{4}$x2+5x(0<x<4).
点评 本题考查了平行线分线段成比例定理、直角梯形面积的计算、矩形的判定与性质;本题难度适中,由平行线分线段成比例定理得出比例式是解决问题的关键.


科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图a是长方形纸带,∠DEF=15°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
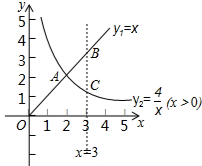 如图所示,函数y1=x(x>0),y2=$\frac{4}{x}$(x>0)的图象交于点A,与直线x=3分别交于B,C两点,给出以下四个结论:
如图所示,函数y1=x(x>0),y2=$\frac{4}{x}$(x>0)的图象交于点A,与直线x=3分别交于B,C两点,给出以下四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1298×104 | B. | 12.98×106 | C. | 1.298×107 | D. | 1.298×103 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com