
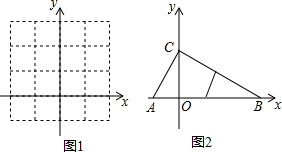
���� ��1���������߽���ʽ�����������Ľ��㣬Ȼ����������
��2���������߽���ʽ��ʾ����������Ľ��㣬��ȫ�������Σ��õ��Ľ��۽������������
��3��������������x��Ľ���������ж������ߵ�ԭ�������εĸ�����
��4�����������ε����Բ��Բ�������ߵĴ�ֱƽ���ߣ����������Ƽ��ɣ�
��� �⣺��1����������y=x2-2x+1��
����������x��Ľ���ΪB��1��0������y��Ľ���ΪC��0��1����
��S=$\frac{1}{2}$��1��1=$\frac{1}{2}$��
�ʴ�Ϊ$\frac{1}{2}$
��2����y=��x-1����x-c����
��A��1��0����B��c��0����
��������y=��x-1����x-c��������c��0��1����������ԭ�������Ρ�ȫ�ȣ�
��١�AOC�ա�BOC��
��AO=BO��
��|c|=1��
��c=1���ᣩ��c=-1��
�ڡ�AOC�ա�COB��
��AO=CO��
���|c|=1��
��c=1���ᣩ��c=-1��
�ʴ�Ϊc=-1
��3��������y=x2+4x+c�ġ�ԭ�������Ρ���
���=16-4c��
�ٵ�����0ʱ������16-4c��0��
��t��4ʱ��û��ԭ�������Σ�
�ڵ���=0ʱ������c=4ʱ��ֻ��һ��ԭ�������Σ�
�۵�����0������c��4��c��0ʱ��������ԭ�������Σ�
��4���ߵ�B�������ǣ�4��0������C�������ǣ�0��2��
��BC����ʽΪy=-$\frac{1}{2}$x+2��
���ABC�����ԲԲ��M��
��M��BC��ֱƽ����l�ϣ�
��l�Ľ���ʽΪy=2x-3��
�ߡ�ODM�ס�CDF��
��$\frac{OM}{CE}=\frac{OD}{CD}$��
��$\frac{OM}{\sqrt{5}}$=$\frac{3}{5}$��
��OM=$\frac{3\sqrt{5}}{5}$��
���ݹ��ɶ����ã�DM=$\frac{6\sqrt{5}}{5}$��
��MF=$\frac{6}{5}$��OF=$\frac{3}{5}$��
��M��$\frac{6}{5}$��$\frac{3}{5}$����
��MҲ��AB�Ĵ�ֱƽ���ߣ�
��A��-$\frac{8}{5}$��0����
�ߵ�A��B��4��0����C��0��2�����������ϣ�
��y=a��x+$\frac{8}{5}$����x-4����
��a=-$\frac{5}{16}$��
��y=-$\frac{5}{16}$x2+$\frac{3}{4}$x+2��
���� �����Ƕ��κ������⣬��Ҫ��������������������Ľ����ȷ��������ȫ�������ε����ʣ��б�ʽ��Ӧ�ã���������ʽ��ȷ�����Ȿ��Ĺؼ�������ԭ�������Σ�


 Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д�
Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д� �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | b��a��c | B�� | b��c��a | C�� | c��b��a | D�� | a��c��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a-2=-$\frac{1}{{a}^{2}}$��a��0�� | B�� | $\sqrt{��-2��^{2}}$=-2 | C�� | a0=0��a��0�� | D�� | $\root{3}{��-2��^{3}}$=-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ���߶�a���Ϧ���
��֪����ͼ���߶�a���Ϧ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��1��x��2 | B�� | x��2��x��1 | C�� | x��2 | D�� | ������ȷ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
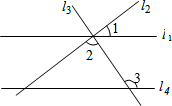 ��ͼ��ֱ��l1��l2��l3����һ�㣬ֱ��l4��l1������3=124�㣬��2=88�㣬���1�Ķ���Ϊ��������
��ͼ��ֱ��l1��l2��l3����һ�㣬ֱ��l4��l1������3=124�㣬��2=88�㣬���1�Ķ���Ϊ��������| A�� | 26�� | B�� | 36�� | C�� | 46�� | D�� | 56�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
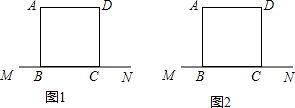 ��֪������ABCD��ͼ��ʾ��M��N��ֱ��BC�ϣ�MB=NC���Էֱ���ͼ1��ͼ2�н����̶ȵ�ֱ����һ����ͬ�ĵ���������OMN��
��֪������ABCD��ͼ��ʾ��M��N��ֱ��BC�ϣ�MB=NC���Էֱ���ͼ1��ͼ2�н����̶ȵ�ֱ����һ����ͬ�ĵ���������OMN���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a8��a4=a2 | B�� | a3•a4=a12 | C�� | $\sqrt{4}$=��2 | D�� | 2x3•x2=2x5 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com