
| A. | $\frac{a+b}{b}$=$\frac{c+d}{d}$ | B. | $\frac{a+c}{c}$=$\frac{b+d}{d}$ | C. | $\frac{a-c}{c}$=$\frac{b-d}{d}$ | D. | $\frac{a-c}{a}$=$\frac{b-d}{d}$ |
分析 先利用比例的基本性质得到则$\frac{a}{b}$=$\frac{c}{d}$或$\frac{a}{c}$=$\frac{b}{d}$,然后根据合分比性质对各选项进行判断.
解答 解:A、ad=bc,则$\frac{a}{b}$=$\frac{c}{d}$,所以$\frac{a+b}{b}$=$\frac{c+d}{d}$,所以A选项计算正确;
B、ad=bc,则$\frac{a}{c}$=$\frac{b}{d}$,所以$\frac{a+c}{c}$=$\frac{b+d}{d}$,所以B选项计算正确;
C、ad=bc,则$\frac{a}{c}$=$\frac{b}{d}$,所以$\frac{a-c}{c}$=$\frac{b-d}{d}$,所以C选项计算正确;
D、ad=bc,则$\frac{a}{c}$=$\frac{b}{d}$,所以$\frac{a-c}{c}$=$\frac{b-d}{d}$,所以D选项计算错误.
故选D.
点评 本题考查了比例的性质:组成比例的四个数,叫做比例的项.两端的两项叫做比例的外项,中间的两项叫做比例的内项


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
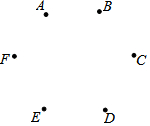 如图,已知点A,B,C,D,E,F最边长为1的正六边形的顶点,在连接两点所得的所有线段中任取一条线段,取到长度为$\sqrt{3}$的线段的概率为( )
如图,已知点A,B,C,D,E,F最边长为1的正六边形的顶点,在连接两点所得的所有线段中任取一条线段,取到长度为$\sqrt{3}$的线段的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若|x|=|y|,则x=y | B. | 若x2=y2,则x=y | C. | 若$\sqrt{x^2}=|y|$,则x=y | D. | 若$\root{3}{x}=\root{3}{y}$,则x=y |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com