
分析 结合二元一次方程组的解法和二次根式的加减法的概念和运算法则进行求解即可.
解答 解:∵$\sqrt{x+y-199}$=-$\sqrt{199-x-y}$,
∴$\sqrt{x+y-199}$+$\sqrt{199-x-y}$=0,
∴x+y=199,
∵m满足$\left\{\begin{array}{l}{2x+3y-m=0,}&{①}\\{3x+2y+1-m=0,}&{②}\end{array}\right.$,
∴①+②得,5(x+y)-2m+1=0,
∵x+y=199,
∴m=498.
点评 本题考查了解二元一次方程组,二次根式的性质,解答本题的关键在于熟练掌握二次根式的性质和二元一次方程组的解法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
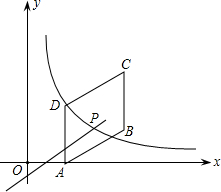 如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=$\frac{k}{x}$的图象经过点D,点P是一次函数y=mx+3-4m(m≠0)的图象与该反比例函数图象的一个公共点;
如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=$\frac{k}{x}$的图象经过点D,点P是一次函数y=mx+3-4m(m≠0)的图象与该反比例函数图象的一个公共点;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{3}{2}$ | C. | -1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
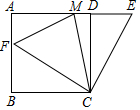 如图,四边形ABCD为正方形,边长为4,E为AD延长线上一点,DE=x(0<x<4),在AE上取一点M,连接CM,将△CME沿CM对折,若点E恰落在线段AB上的点F处,则AM=$\frac{8x}{4+x}$.
如图,四边形ABCD为正方形,边长为4,E为AD延长线上一点,DE=x(0<x<4),在AE上取一点M,连接CM,将△CME沿CM对折,若点E恰落在线段AB上的点F处,则AM=$\frac{8x}{4+x}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com