
分析 (1)根据负整数指数幂的意义即可求出答案.
(2)根据分式的乘除法即可求出答案
(3)根据分式的加减运算以及乘除运算即可求出答案
(4)根据零指数幂的意义、负整数指数幂,实数运算法则即可求出答案.
解答 解:(1)原式=a6b4•a-3b-9=a3b-5=$\frac{{a}^{3}}{{b}^{5}}$
(2)原式=$\frac{a(a-b)}{{a}^{2}}$÷$\frac{{a}^{2}-{b}^{2}}{ab}$
=$\frac{a-b}{a}$×$\frac{ab}{(a-b)(a+b)}$
=$\frac{b}{a+b}$
(3)原式=(a-3-$\frac{7}{a+3}$)×$\frac{2(a+3)}{a-4}$
=(a-3)×$\frac{2(a+3)}{a-4}$-$\frac{14}{a-4}$
=$\frac{2({a}^{2}-9)-14}{a-4}$
=2a+8
(4)原式=1-$\frac{1}{4}$+$\frac{1}{4}$+1
=2
点评 本题考查学生的运算能力,解题的关键是熟练运用运算法则,本题属于基础题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | n2-1 | B. | 12+22+32+…+i2-i | ||
| C. | 12+22+32+…+n2-1 | D. | 12+22+32+…+n2-(1+2+3+…+n ) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
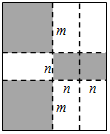 如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.
如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
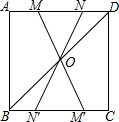 如图,在正方形ABCD中,连接BD,点O是BD的中点,若点M、N是边AD上的两点,连接MO,NO,并分别延长与边BC相交于点M′,N′.
如图,在正方形ABCD中,连接BD,点O是BD的中点,若点M、N是边AD上的两点,连接MO,NO,并分别延长与边BC相交于点M′,N′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
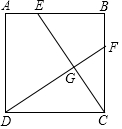 如图,正方形ABCD中,AE=BF.
如图,正方形ABCD中,AE=BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com