
达州市凤凰小学位于北纬21°,此地一年中冬至日正午时刻,太阳光与地面的夹角最小,约为35.5°;夏至日正午时刻, 太阳光的夹角最大,约为82.5°。己知该校一教学楼窗户朝南,窗高207cm,如图(1)请你为该窗户设计一个直角形遮阳棚BCD,如图(2)所示,要求最大限度地节省材料,夏至日正
太阳光的夹角最大,约为82.5°。己知该校一教学楼窗户朝南,窗高207cm,如图(1)请你为该窗户设计一个直角形遮阳棚BCD,如图(2)所示,要求最大限度地节省材料,夏至日正 午刚好遮住全部阳光,冬至日正午能射入室内的阳光没有遮挡。
午刚好遮住全部阳光,冬至日正午能射入室内的阳光没有遮挡。
(1)在图(3)中画出设计草图;
(2)求BC、CD的长度(结果精确到个位)
(参考数据: sin35.5°≈0.58, cos35.5°≈0.81, tan35.5°≈0.71, sin82.5°≈0.99,cos82.5°≈0 .13,tan82.5°≈7.60)
.13,tan82.5°≈7.60)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
已知一只纸箱中装有除颜色外完全相同的红色、黄色、蓝色乒乓球共100个.
从纸箱中任意摸出一球,摸到红色球、黄色球的概率分别是0.2、0.3.
(1 )试求出纸箱中蓝色球的个数;
)试求出纸箱中蓝色球的个数;
(2)小明向纸箱中再放进红色球若干个,小丽为了估计放入的红球的个数,她将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到红球的频率在0.5附近波动,请据此估计小明放入的红球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
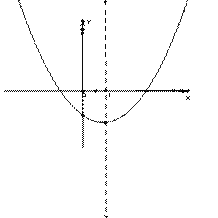
右图是二次函数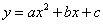 的图象的一部分,对称轴是直线X=1
的图象的一部分,对称轴是直线X=1
① b2>4ac ② 4a-2b+c<0③ 不等式ax2+bx+c>0的解集是x≥3.5④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2上述4个判断中,正确的是
A.①② B. ①④ C.①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
x1,x2是关于x的一元二次方程x2﹣mx+m﹣2=0的两个实数根,是否存在实数m使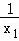 +
+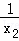 =0成立?则正确的是结论是( )
=0成立?则正确的是结论是( )
|
| A. | m=0时成立 | B. | m=2时成立 | C. | m=0或2时成立 | D. | 不存在 |
查看答案和解析>>
科目:初中数学 来源: 题型:
给定直线l:y=kx,抛物线C:y=ax2+bx+1.
(1)当b=1时,l与C相交于A,B两点,其中A为C的顶点,B与A关于原点对称,求a的值;
(2)若把直 线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点.
线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点.
①求此抛物线的解析式;
②若P是此抛物线上任一点,过P作PQ∥y轴且与直线y=2交于Q点,O为原点.求证:OP=PQ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com