
分析 依次求出S1、S2、…,即可发现规律:Sn=$\frac{1}{n(n+1)}$,最后计算s1+s2+s3+…+sn即可.
解答 解:当n=1时,y=-$\frac{1}{2}$x+$\frac{\sqrt{2}}{2}$,
此时,A(0,$\frac{\sqrt{2}}{2}$),B($\sqrt{2}$,0),
∴S1=$\frac{1}{2}$×$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=$\frac{1}{1×2}$,
同理可得,S2=$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{2}}{3}$=$\frac{1}{2×3}$,
…
∴Sn=$\frac{1}{2}$×$\frac{\sqrt{2}}{n}$×$\frac{\sqrt{2}}{n+1}$=$\frac{1}{n(n+1)}$,
∴s1+s2+s3+…+sn=$\frac{1}{1×2}$×$\frac{1}{2×3}$×…×$\frac{1}{n(n+1)}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.
故答案为:$\frac{n}{n+1}$
点评 本题考查了一次函数图象上点的坐标特征.注意发现规律:Sn=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$是解此题的关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
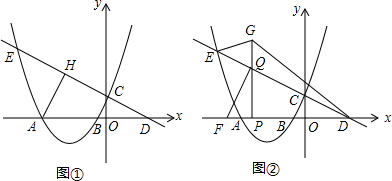
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
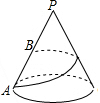 已知圆锥底面半径为1,母线长为4,地面圆周上有一点A,一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B,则蚂蚁爬行的最短路程为2$\sqrt{5}$(结果保留根号)
已知圆锥底面半径为1,母线长为4,地面圆周上有一点A,一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B,则蚂蚁爬行的最短路程为2$\sqrt{5}$(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
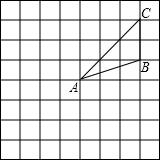 如图所示,在边长为1的网格中,△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.
如图所示,在边长为1的网格中,△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
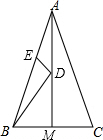 如图,△ABC中,AB=AC=4,∠BAC=45°,AM平分∠BAC,点D、E 分别为AM、AB上的动点,则BD+DE的最小值是2$\sqrt{2}$.
如图,△ABC中,AB=AC=4,∠BAC=45°,AM平分∠BAC,点D、E 分别为AM、AB上的动点,则BD+DE的最小值是2$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com