练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】抛物线的图象先向右平移个单位再向下平移个单位，所得图象的解析式为，则____________

    【答案】0

    【解析】

    利用反向平移：先把y=x2-2x-3配成顶点得到y=（x-1）2-4，得到抛物线y=x2-2x-3的顶点坐标为（1，-4），通过点（1，-4）先向左平移2个单位再向上平移3个单位得到点的坐标为（-1，-1），然后利用顶点式写出平移后的抛物线解析式，再把解析式化为一般式即可得到b和c的值．

    ∵y=x2-2x-3=（x-1）2-4，

    ∴抛物线y=x2-2x-3的顶点坐标为（1，-4），

    把点（1，-4）先向左平移2个单位再向上平移3个单位得到点的坐标为（-1，-1），

    ∴平移后的抛物线解析式为y=（x+1）2-1=x2+2x，

    所以b=2，c=0,

    所以bc=0.

    故答案为：0.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，抛物线y＝ax2＋bx－2与x轴交于点A(－3,0)、B(1,0)，与y轴交于点C．

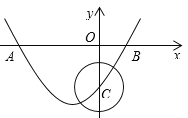
    （1）求抛物线的函数表达式．

    （2）在抛物线上是否存在点D，使得△ABD的面积等于△ABC的面积的倍？若存在，求出点D的坐标；若不存在，请说明理由．

    （3）若点E是以点C为圆心且1为半径的圆上的动点，点F是AE的中点，请直接写出线段OF的最大值和最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝ax2﹣4ax+3a．

    (1)若a=1,则函数y的最小值为_______.

    (2)当1≤x≤4时，y的最大值是4，则a的值为_______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知反比例函数与一次函数，其中与的部分对应值如下表：

    （1）求，的值，并将表格补充完整；

    （2）在直角坐标系中，画出一次函数和反比例函数的图象；

    （3）直接写出不等式的解

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与x轴相交于A（3，0）、B两点，与y轴交于点C（0，3），点B在x轴的负半轴上，且.

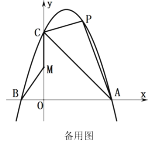
    （1）求抛物线的函数关系式；

    （2）若P是抛物线上且位于直线上方的一动点，求的面积的最大值及此时点P的坐标；

    （3）在线段上是否存在一点M，使的值最小？若存在，请求出这个最小值及对应的M点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，对称轴为直线x＝﹣1的抛物线y＝ax2+bx+c（a≠0）与x轴相交于A、B两点，其中点A的坐标为（﹣3，0）．

    （1）求点B的坐标；

    （2）已知a＝1，C为抛物线与y轴的交点，若点P在抛物线上，且S△POC＝4S△BOC．求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2018年非洲猪瘟疫情暴发后，今年猪肉价格不断走高，引起了民众与政府的高度关注，据统计：今年7月20日猪肉价格比今年年初上涨了60%，某市民今年7月20日在某超市购买1千克猪肉花了80元钱．

    （1）问：今年年初猪肉的价格为每千克多少元？

    （2）某超市将进货价为每千克65元的猪肉，按7月20日价格出售，平均一天能销售出100千克，经调查表明：猪肉的售价每千克下降1元，其日销售量就增加10千克，超市为了实现销售猪内每天有1560元的利润，并且可能让顾客得到实惠，猪肉的售价应该下降多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，点A在y轴上，∠OAB＝30°，B（2，0），OC⊥AB于点C，点C在反比例函数y＝（k≠0）的图象上．

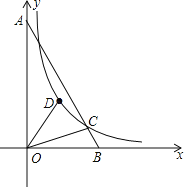
    （1）求该反比例函数解析式；

    （2）若点D为反比例函数y＝（k≠0）在第一象限的图象上一点，且∠DOC＝30°，求点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB为⊙O的直径，CD切⊙O于C点，弦CF⊥AB于E点，连结AC．

    （1）求证：∠ACD=∠ACF；

    （2）当AD⊥CD，BE=2cm，CF=8cm，求AD的长．

    查看答案和解析>>

    同步练习册答案