
【题目】某厂家在甲、乙两商场销售同一件商品所获得的利润分别为![]() ,(单位:元),
,(单位:元),![]() 与销售量
与销售量![]() (单位:件)的函数关系图象如图所示,试根据图像解决下列问题:
(单位:件)的函数关系图象如图所示,试根据图像解决下列问题:

(1)分别求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)现厂家分配该商品800件给甲商场、400件给乙商场,当甲、乙两商场售完这批商品后,厂家可获得总利润多少元?
【答案】(1)y甲=0.8x;当0≤x≤200时,y乙=2x ;当x>200时,y乙=0.2x+360(2)1080元
【解析】
(1)设y甲=k1x(k1≠0),把x=600,y甲=480代入即可;当0≤x≤200时,设y乙=k2x(k2≠0),把x=200,y乙=400代入即可;当x>200时,设y乙=k3x+b(k3≠0),把x=200,y乙=400和x=600,y乙=480代入即可;
(2)当x=800时求出y甲,当x=400时求出y乙,即可求出答案.
(1)解:(1)设y甲=k1x(k1≠0),由图象可知:
当x=600时,y甲=480,代入得:480=600k1,解得:k1=0.8,
所以y甲=0.8x;
当0≤x≤200时,设y乙=k2x(k2≠0),
由图象可知:
当x=200时,y乙=400,
代入得:400=200k2,
解得:k2=2,
所以y乙=2x;
当x>200时,设y乙=k3x+b(k3≠0),
由图象可知:由图象可知:
当x=200时,y乙=400,
当x=600时,y乙=480,
代入得:
解得:k3=0.2,b=360,
所以y乙=0.2x+360;
即y乙=
(2)∵当x=800时,y甲=0.8×800=640;
当x=400时,y乙=0.2×400+360=440,
∴640+440=1080,
答:厂家可获得总利润是1080元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知面积为12的长方形ABCD,一边AB在数轴上。点A表示的数为—2,点B表示的数为1,动点P从点B出发,以每秒1个单位长度的速度沿数轴向左匀速运动,设点P运动时间为t(t>0)秒.

(1)长方形的边AD长为 单位长度;
(2)当三角形ADP面积为3时,求P点在数轴上表示的数是多少;
(3)如图2,若动点Q以每秒3个单位长度的速度,从点A沿数轴向右匀速运动,与P点出发时间相同。那么当三角形BDQ,三角形BPC两者面积之差为![]() 时,直接写出运动时间t 的值.
时,直接写出运动时间t 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种笔记本的售价是每本2.2元,如果买100本以上,超过100本的部分售价每本2元.
(1)若买100本要花 元,买200本要花 元.
(2)若童威班上买这种笔记本花了n元,试问:
①童威班上买了这种笔记本多少本?(用n的式子表示)
②如果童威班上买这种笔记本恰好是0.48n本,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知![]() 是关于
是关于![]() 的方程
的方程![]() 的解,求
的解,求![]() 的值.
的值.
(2)已知关于x的方程![]() 的解与方程
的解与方程![]() 的解互为倒数,求
的解互为倒数,求![]() 的值.
的值.
(3)小丽在解关于![]() 的方程
的方程![]() 时,出现了一个失误:“在将
时,出现了一个失误:“在将![]() 移到方程的左边时,忘记了变号.”结果她得到方程的解为
移到方程的左边时,忘记了变号.”结果她得到方程的解为![]() ,求
,求![]() 的值和原方程的解.
的值和原方程的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
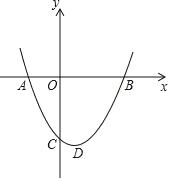
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴相交于点A(﹣2,0)和点B,与y轴相交于点C,顶点D(1,﹣ ![]() ).
).
(1)求抛物线的解析式;
(2)求四边形ACDB的面积;
(3)若(1)中的抛物线只进行上下平移或者左右平移,使平移后的抛物线与坐标轴仅有两个交点,请直接写出平移后的抛物线的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
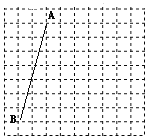
【题目】如图,方格纸中每个小正方形的边长均为1.线段AB的两个端点在小正方形的顶点上。
(1)在图中画一个以AB为腰的等腰三角形△ABC,点C在小正方形的顶点上,且tan∠B=3;
(2)在图中画一个以AB为底的等腰三角形△ABD,点D在小正方形的项点上,且△ABD是锐角三角形.连接CD,请直接写出线段CD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2015年5月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见下表.若2015年5月份,该市居民甲用电100千瓦时,交电费60元.
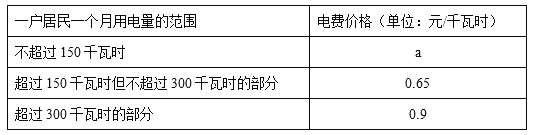
(1)上表中,a= ,若居民乙用电200千瓦时,交电费 元.
(2)若某用户某月用电量超过300千瓦时,设用电量为x千瓦时,请你用含x的代数式表示应交的电费.
(3)试行“阶梯电价”收费以后,该市一户居民月用电多少千瓦时时,其当月的平均电价每千瓦时不超过0.62元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
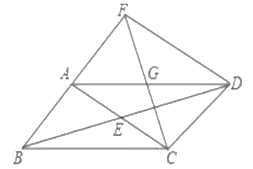
(1)求证:![]() ;
;
(2)若![]() ,∠BCD=120°判断四边形
,∠BCD=120°判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四点A、B、C、D;
(1)画射线AD;(不需写作图过程)
(2)求作点P,使PA+PB+PC+PD的值最小;(不需写作图过程)
(3)在(2)的条件下,若S△ABP=2,S△ADP=6,S△BCP=1.5,则S△DCP= .
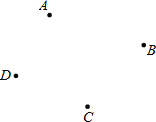
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com