
如图,正三角形ABC的边长为3+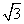 .
.
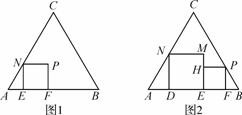
(1)如图1,正方形EFPN的顶点E,F在边AB上,顶点N在边AC上,在正三角形ABC及其内部,以A为位似中心,作正方形EFPN的位似正方形E′F′P′N′,且使正方形E′F′P′N′的面积最大(不要求写作法);
(2)求(1)中作出的正方形E′F′P′N′的边长;
(3)如图2,在正三角形ABC中放入正方形DEMN和正方形EFPN,使得DE,EF在边AB上,点P,N分别在边CB,CA上,求这两个正方形面积和的最大值和最小值,并说明理由.
解:(1)如图①,正方形E′F′P′N′即为的所求.( 4分)
4分)
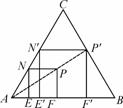 图(1)
图(1)
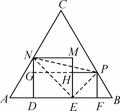 图(2)
图(2)
(2)设正方形E′F′P′N′的边长为x.
∵△ABC为正三角形,∴AE′=BF′=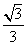 x.
x.
 ∴x+
∴x+ x=3+
x=3+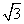 .∴x=
.∴x=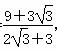 ,即x=3
,即x=3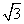 -3.(8分)
-3.(8分)
(没有分母有理化也对,x≈2.20也正确)
(3)如图(2),连接NE,EP,PN,则∠NEP=90°.
设正方形DEMN、正方形EFPH的边长分别为m、n(m≥n),它们的面积和为S,则NE=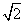 m,PE=
m,PE=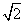 n.
n.
∴PN2=NE2 +PE2=2m2+2n2=2(m2+n2),
+PE2=2m2+2n2=2(m2+n2),
∴S=m2+n2=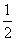 PN2.
PN2.
延长PH交ND于点G,则PG⊥ND.
在Rt△PGN中,PN2=PG2+GN2=(m+n)2+(m-n)2.
∵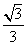 m+m+n+
m+m+n+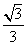 n=
n=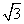 +3,
+3,
即m+n=3,∴S=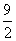 +
+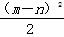
①当(m-n)2=0,即m=n时,S最小,∴S最小=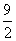 .
.
②当(m-n)2最大,即当m最大且n最小时,S最大
∵m+n=3,
由(2)知,m最大=3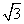 -3,
-3,
∴n最小=3-m最大=3-(3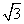 -3)
-3) =6-3
=6-3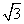 .(16分)
.(16分)
∴S最大=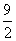 +
+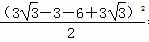 =99-54
=99-54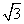 .(S最大≈5.47也正确)(18分)
.(S最大≈5.47也正确)(18分)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
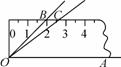
如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰为2 cm,若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数为______cm(结果精确到0.1 cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
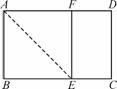
已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=( )
A . 
 B.
B. 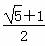 C.
C.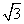 D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
某星球 的体积约为6 635 421 km3,用科学计数法(保留三个有效数字)表示为6.64×10n km3,则n=( )
的体积约为6 635 421 km3,用科学计数法(保留三个有效数字)表示为6.64×10n km3,则n=( )
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com