
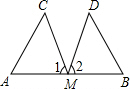
 已知:如图,M是AB的中点,∠1=∠2,MC=MD.求证:△ACM≌△BDM.
已知:如图,M是AB的中点,∠1=∠2,MC=MD.求证:△ACM≌△BDM.科目:初中数学 来源: 题型:
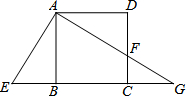 如图,四边形ABCD是正方形,点E在CB的延长线上,连结AE,将△ABE绕点A逆时针旋转90°,得到△ADF,点E落在DC上的点F处,AF的延长线交BC延长线于点G.若AB=3,AE=
如图,四边形ABCD是正方形,点E在CB的延长线上,连结AE,将△ABE绕点A逆时针旋转90°,得到△ADF,点E落在DC上的点F处,AF的延长线交BC延长线于点G.若AB=3,AE=| 13 |
| A、1.5 | B、1.6 |
| C、1.8 | D、2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
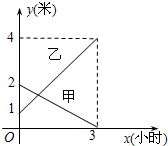 自来水公司有甲、乙两个蓄水池,现将甲池的中水匀速注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如下所示,结合图象回答下列问题.
自来水公司有甲、乙两个蓄水池,现将甲池的中水匀速注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如下所示,结合图象回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E、F,要使△ABF≌△CDE,需添加个条件,可以是( )
如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E、F,要使△ABF≌△CDE,需添加个条件,可以是( )| A、① | B、①或② |
| C、①或②或④ | D、四个条件中的任意一个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
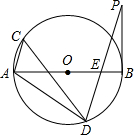 如图,AB是⊙O的直径,点A、C、D在⊙O上,过D作PD∥AC交AB于E,且∠BPD=∠ADC.
如图,AB是⊙O的直径,点A、C、D在⊙O上,过D作PD∥AC交AB于E,且∠BPD=∠ADC.查看答案和解析>>
科目:初中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com