
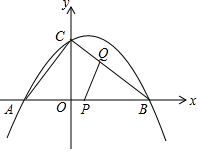
 综合与探究:如图,抛物线y=ax2+bx+$\frac{12}{5}$与x轴交于A(-$\frac{9}{5}$,0),B($\frac{16}{5}$,0)两点,与y轴交于点C,连接AC,BC,一动点P从点A出发,沿线段AB向终点B以每秒1个单位长度的速度运动;同时,点Q从点B出发,以相同的速度沿线段BC向终点C运动,当其中一个动点到达终点时,另一个动点也随之停止运动,连接PQ.设P,Q两点运动时间为t秒.
综合与探究:如图,抛物线y=ax2+bx+$\frac{12}{5}$与x轴交于A(-$\frac{9}{5}$,0),B($\frac{16}{5}$,0)两点,与y轴交于点C,连接AC,BC,一动点P从点A出发,沿线段AB向终点B以每秒1个单位长度的速度运动;同时,点Q从点B出发,以相同的速度沿线段BC向终点C运动,当其中一个动点到达终点时,另一个动点也随之停止运动,连接PQ.设P,Q两点运动时间为t秒.分析 (1)先求得点C的坐标,设抛物线的解析式为y=a(x+$\frac{9}{5}$)(x-$\frac{16}{5}$),将点C的坐标代入求得a的值即可;
(2)分为PB=QB、PQ=QB、PQ=PB三种情况进行解答即可;
(3)过点Q作QD⊥OB,垂足为D.先用含t的式子表示出PB、QD的长,然后依据四边形APQC的面积=△ABC的面积-△PBQ的面积列出四边形的面积与t的函数关系式,依据二次函数的性质可知当t=$\frac{5}{2}$时四边形的面积最小,然后再说明四边形DPBQ为菱形,然后可求得点D的坐标,然后可判断出点D是否在抛物线上.
解答 解:(1)将x=0代入抛物线的解析式得:y=$\frac{12}{5}$,
∴C(0,$\frac{12}{5}$).
设抛物线的解析式为y=a(x+$\frac{9}{5}$)(x-$\frac{16}{5}$).
将点C的坐标代入得:-$\frac{144}{25}$a=$\frac{12}{5}$,解得:a=-$\frac{12}{5}$.
∴抛物线的解析式为y=-$\frac{5}{12}$x2+$\frac{7}{12}$x+$\frac{12}{5}$.
(2)当PB=QB时.
∵PB=AB-AP=5-t,QB=t,
∴5-t=t,解得t=$\frac{5}{2}$.
如图1当PQ=QB时,过点Q作QD⊥PB.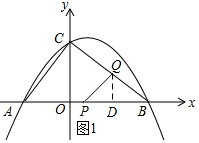
∵PQ=QB,QD⊥PB,
∴PD=BD.
∴BD=$\frac{1}{2}$PB.
∴$\frac{4}{5}$t=$\frac{1}{2}$(5-t),解得:t=$\frac{25}{13}$.
如图2所示:当PQ=PB时,作PD⊥QB,垂足为D.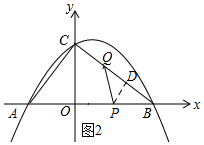
∵PQ=PB,PD⊥QB,
∴QD=BD.
∴DB=$\frac{1}{2}$QB.
∴$\frac{1}{2}$t=$\frac{4}{5}$(5-t),解得t=$\frac{40}{13}$.
综上所述,当t的值$\frac{5}{2}$或$\frac{40}{13}$或$\frac{25}{13}$时,△PBQ为等腰三角形.
(3)点 D 不在抛物线上.
理由:如图3所示:过点Q作QD⊥OB,垂足为D.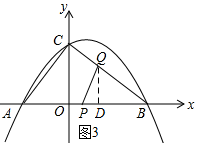
∵QD=$\frac{3}{5}$QB=$\frac{3}{5}t$,PB=5-t,
∴△PBQ的面积=$\frac{1}{2}$×$\frac{3}{5}$t(5-t)=-$\frac{3}{10}$t2+$\frac{3}{2}$t.
∵AB=5,OC=$\frac{12}{5}$,
∴△ABC的面积=$\frac{1}{2}$×5×$\frac{12}{5}$=6.
∴四边形APQC的面积=△ABC的面积-△PBQ的面积=6-(-$\frac{3}{10}$t2+$\frac{3}{2}$t)=$\frac{3}{10}$t2-$\frac{3}{2}$t+6.
∴当t=$\frac{5}{2}$时,四边形APQC的面积有最小值.
∵BD=$\frac{3}{5}$BQ=$\frac{3}{5}$×$\frac{5}{2}$=$\frac{3}{2}$,BD=$\frac{4}{5}$QB=2,
∴点Q($\frac{6}{5}$,$\frac{3}{2}$).
∵当t=$\frac{5}{2}$时,PB=QB,
∴四边形DPBQ为菱形,
∴D(-$\frac{13}{10}$,$\frac{3}{2}$).
∵点D的坐标不符抛物线的解析式,
∴点D不在抛物线上.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、二次函数的性质、翻折的性质,分类讨论是解答问题(2)的关键,证得四边形DPBQ为菱形,然后依据菱形的性质求得点D的坐标是解答问题(3)的关键.


科目:初中数学 来源: 题型:解答题
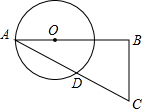 如图所示,BD是⊙O的切线,AE是⊙O的直径,AD是一条非直径的弦,过点B作BC⊥AB,BC与AD的延长线相交于点C,
如图所示,BD是⊙O的切线,AE是⊙O的直径,AD是一条非直径的弦,过点B作BC⊥AB,BC与AD的延长线相交于点C,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
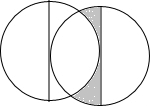 半径为1的两圆放置位置如图所示,一圆的直径恰好是另一圆的切线,圆心均为切点,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
半径为1的两圆放置位置如图所示,一圆的直径恰好是另一圆的切线,圆心均为切点,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
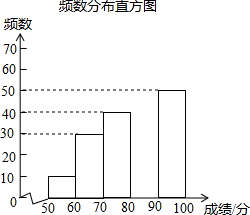 为了传承优秀传统文化,我县团委组织了一次全县有3000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
为了传承优秀传统文化,我县团委组织了一次全县有3000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:| 成绩x/分 | 频数 | 频率 |
| 50≤x<60 | 10 | 0.05 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 40 | n |
| 80≤x<90 | m | 0.35 |
| 90≤x≤100 | 50 | 0.25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
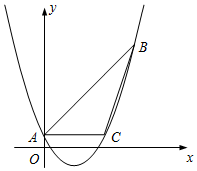 如图,已知抛物线y=ax2-2x+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴.
如图,已知抛物线y=ax2-2x+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -5 | -4 | -3 | -2 | -1 | … |
| y | … | -7.5 | -2.5 | 0.5 | 1.5 | 0.5 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com