
 已知正方形OABC,BEFG,按照如图所示位置摆放在数轴上,点O、A、E表示的数分别为1、2、3,若以O为圆心,OF为半径作圆弧,则与数轴的交点表示的数为$\sqrt{10}+1$、-$\sqrt{10}+1$.
已知正方形OABC,BEFG,按照如图所示位置摆放在数轴上,点O、A、E表示的数分别为1、2、3,若以O为圆心,OF为半径作圆弧,则与数轴的交点表示的数为$\sqrt{10}+1$、-$\sqrt{10}+1$. 分析 过点F作FH⊥数轴于点H,连接OF,证明△ABE≌△HEF.所以AB=EH=1,FH=AE=1,所以OH=3,根据勾股定理$OF=\sqrt{O{H}^{2}+F{H}^{2}}=\sqrt{{3}^{2}+{1}^{2}}=\sqrt{10}$,即可解答.
解答 解:如图,过点F作FH⊥数轴于点H,连接OF,
在Rt△BAE中,AB=1,AE=1,
∵OABC,BEFG为正方形,
∴∠BAE=∠BEF=90°,BE=FE,
∴∠ABE+∠AEB=90°,∠AEB+∠FEH=90°,
∴∠ABE=∠FEH,
在△ABE和△HEF中,
$\left\{\begin{array}{l}{∠ABE=∠FEH}\\{∠BAE=∠FHE}\\{BE=FE}\end{array}\right.$
∴△ABE≌△HEF.
∴AB=EH=1,FH=AE=1,
∴OH=3,
∴$OF=\sqrt{O{H}^{2}+F{H}^{2}}=\sqrt{{3}^{2}+{1}^{2}}=\sqrt{10}$,
若以O为圆心,OF为半径作圆弧,则与数轴的交点表示的数为1+$\sqrt{10}$、1-$\sqrt{10}$.
点评 考查了正方形的性质,勾股定理和实数与数轴,得出OF的长是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | m<0 | B. | m>0 | C. | m<$\frac{1}{2}$ | D. | m>$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
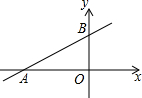 如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )| A. | x>-3 | B. | x<-3 | C. | x>3 | D. | x<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
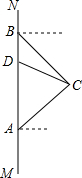 如图,在南北方向的海岸线MN上,有A、B两艘巡船,现均收到故障船C的求救信号.已知A.B两船相距100($\sqrt{3}$+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.已知距观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,在南北方向的海岸线MN上,有A、B两艘巡船,现均收到故障船C的求救信号.已知A.B两船相距100($\sqrt{3}$+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.已知距观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不论x取何值,分式都有意义 | B. | 分式的值可以等于1 | ||
| C. | 不论x取何值,分式值都不为0 | D. | 当x=0或-1时,分式无意义 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )
如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )| A. | 45 | B. | 5 | C. | $\frac{1}{5}$ | D. | $\frac{1}{45}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
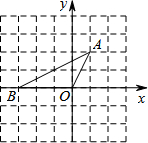 如图,把直角坐标系xOy放置在边长为1的正方形网格中,O是坐标原点,点A、O、B均在格点上,将△OAB绕O点按顺时针方向旋转90°后,得到△OA′B′.
如图,把直角坐标系xOy放置在边长为1的正方形网格中,O是坐标原点,点A、O、B均在格点上,将△OAB绕O点按顺时针方向旋转90°后,得到△OA′B′.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{25}{40}$ | B. | $\frac{24}{41}$ | C. | $\frac{23}{40}$ | D. | $\frac{25}{41}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com