
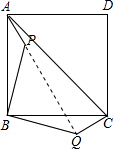
 如图,已知P为正方形ABCD内一点,△ABP经过旋转后到达△CBQ的位置.
如图,已知P为正方形ABCD内一点,△ABP经过旋转后到达△CBQ的位置.| 2 |
| 2 |
| 34 |
| 34 |
| 17 |
| 2 |
| 2 |
| 2 |
| AQ2+CQ2 |
| 34 |
| 34 |
| AC | ||
|
| 17 |
90•π•(
| ||
| 360 |
90•π•(
| ||
| 360 |
| 15 |
| 4 |


科目:初中数学 来源: 题型:
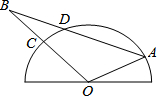 如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠B的度数为( )
如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠B的度数为( )| A、20° | B、30° |
| C、45° | D、60° |
查看答案和解析>>
科目:初中数学 来源: 题型:
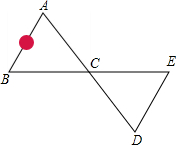 如固,为修筑一条公路,需测量出被大石头阻挡的∠BAC的大小,为此,小张师傅便在直线AC上取点D,使AC=CD,在BC的延长线上取点E,使BC=CE,连接DE,只要测出∠D的度数,则可知∠A的度数等于∠D的度数.请说明理由.
如固,为修筑一条公路,需测量出被大石头阻挡的∠BAC的大小,为此,小张师傅便在直线AC上取点D,使AC=CD,在BC的延长线上取点E,使BC=CE,连接DE,只要测出∠D的度数,则可知∠A的度数等于∠D的度数.请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com