
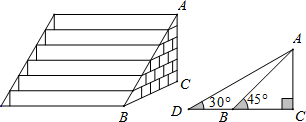
分析 (1)在直角三角形ABC中利用三角函数即可求得AC、然后在直角三角形ADC中求得AD的长,AD-AB即是所求的解.
(2)在Rt△ABC中,由BC=AB•cos45°求得BC长,再由CD=$\frac{AC}{tan30°}$求得CD的长,根据BD=CD-BC可得答案.
解答 解:(1)∵在直角三角形ABC中,AC=ABsin45°=$\frac{5\sqrt{2}}{2}$(m)
在直角三角形ADC中,AD=$\frac{AC}{sin30°}$=$\frac{5\sqrt{2}}{2}$÷$\frac{1}{2}$=5$\sqrt{2}$(米),
∴AD-AB=(5$\sqrt{2}$-5)(米)≈5×(1.414-1)=2.07≈2.1(米).
即改善后的台阶坡面加长约2.1米.
(2)如图,在Rt△ABC中,BC=AB•cos45°=5cos45°=$\frac{5\sqrt{2}}{2}$(米).
在Rt△ACD中,CD=$\frac{AC}{tan30°}$=$\frac{\frac{5\sqrt{2}}{2}}{\frac{\sqrt{3}}{3}}$=$\frac{5\sqrt{6}}{2}$(米).
∴BD=CD-BC=$\frac{5\sqrt{6}}{2}$-$\frac{5\sqrt{2}}{2}$≈2.6(米).
答:改善后的台阶多占2.6米长的一段水平地面.
点评 本题考查了解直角三角形,理解两个直角三角形有公共的直角边,先求出公共边的解决此类题目的基本出发点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
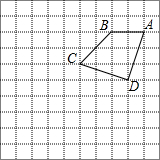 如图,在正方形网格图中,点A、B、C、D均在格点上,以点A为位似中心,将四边形ABCD放大到原来的2倍得到四边形AB′C′D′.
如图,在正方形网格图中,点A、B、C、D均在格点上,以点A为位似中心,将四边形ABCD放大到原来的2倍得到四边形AB′C′D′.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-3)2=19 | B. | (x-3)2=1 | C. | (x+3)2=19 | D. | (x+3)2=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com