
【题目】(1)在下列表格中填上相应的值
x | … | -6 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 6 | … |
| … | -1 | -2 | 3 | 1 | … |

(2)若将上表中的变量![]() 用y来代替(即有
用y来代替(即有![]() ),请以表中的
),请以表中的![]() 的值为点的坐标, 在下方的平面直角坐标系描出相应的点,并用平滑曲线顺次连接各点
的值为点的坐标, 在下方的平面直角坐标系描出相应的点,并用平滑曲线顺次连接各点
(3)在(2)的条件下,可将y看作是x的函数 ,请你结合你所画的图像,写出该函数图像的两个性质 :__________________________________________________.
(4)结合图像,借助之前所学的函数知识,直接写出不等式![]() 的解集: ____________
的解集: ____________
【答案】 该函数图形是一个轴对称(中心对称)(即是轴对称又是中心对称)图形 ![]() 或
或![]()
【解析】分析:(1)计算后完成表格即可;
(2)作出函数图象即可;
(3)根据图象得出函数的性质即可;
(4)再同一坐标系中,作出![]() 和y=x+1的图象,求出交点A,B的坐标,根据图象得出结论,
和y=x+1的图象,求出交点A,B的坐标,根据图象得出结论,
详解:(1)填表如下:
x | … | -6 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 6 | … |
| … | -1 | - | -2 | -3 | -6 | 6 | 3 | 2 |
| 1 | … |
(2)如图:
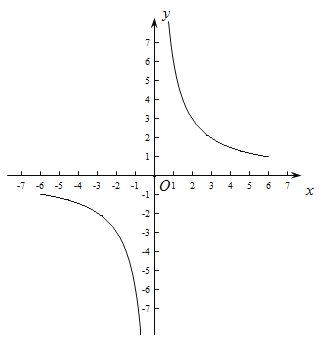
(3) 本题答案是开放式的,学生答出某两个性质即可:
如从函数图像对称性来说:该函数图形是一个轴对称(中心对称)(即是轴对称又是中心对称)图形或该函数经过一、三象限或该函数在每个象限内,y随x增大而增小(x>0 或x<0, y随x增大而增小)等或与x轴y轴无交点;
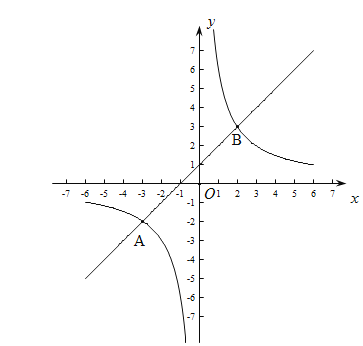
(4)再同一坐标系中,作出![]() 和y=x+1的图象,如图所示, 解得:A(-3,-2),B(2,3), 由图象可知:不等式
和y=x+1的图象,如图所示, 解得:A(-3,-2),B(2,3), 由图象可知:不等式![]() 的解集为:
的解集为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1 , x2 .
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数-2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数-2017将与圆周上的哪个数字重合( )
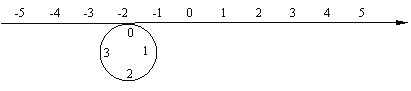
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )

A、120° B、135° C、150° D、45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C
与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C ![]() 在抛物线上,直线AC与y轴交于点D.
在抛物线上,直线AC与y轴交于点D.
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴的正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m , 求AN的长(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题12分)如图1,在平面直角坐标系中,四边形OABC各顶点的坐标分别O(0,0),A(3, ![]() ),B(9,5
),B(9,5 ![]() ),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3,
),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3, ![]() ,
, ![]() (单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.
(单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.
(1)求AB所在直线的函数表达式.
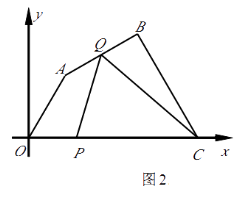
(2)如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值.
(3)在P,Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的括号内
![]() , -
, -![]() , 0,
, 0, ![]() ,‐3.1415926, 20%, ‐3
,‐3.1415926, 20%, ‐3![]() , 2, -1,3.1010010001…(每两个1之间逐次增加1个0)
, 2, -1,3.1010010001…(每两个1之间逐次增加1个0)
①正数集合{ ……}
②负数集合{ ……}
③整数集合{ ……}
④负分数集合{ ……}
⑤无理数集合{ ……}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com