
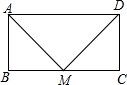
 如图所示,矩形ABCD中,M是BC的中点,且MA⊥MD,若矩形的周长为36cm,求此矩形的面积.
如图所示,矩形ABCD中,M是BC的中点,且MA⊥MD,若矩形的周长为36cm,求此矩形的面积. 分析 根据矩形的性质求出∠CDM=∠BMA,∠DMC=∠BAM继而求出△DCM∽△MBA.然后求出AB=BM,(AB+2AB)×2=36可求出AB,BC的值.最后可求出矩形ABCD的面积.
解答 解:∠CDM+∠CMD=90°,∠CMD+∠BMA=90°,
∴∠CDM=∠BMA,同理∠DMC=∠BAM.
∴△DCM∽△MBA.
∴$\frac{DC}{MB}$=$\frac{CM}{AB}$,
∵DC=AB,BM=CM,
∴AB=BM.
又∵(AB+BC)×2=36,
∴(AB+2AB)×2=36.
∴AB=6,BC=12.
∴矩形ABCD的面积为6×12=72(cm2).
点评 本题的关键是利用了三角形相似的判定定理,及相似三角形的性质和矩形的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com