Question

已知圆中一弦将圆分为1：2的两条弧，则这条弦所对的圆心角为    度．

Answer 1

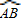
【答案】分析：根据题意画出相应的图形，由弦AB将圆分为1：2的两条弧，利用弧与圆心角的关系，得到优弧与劣弧所对圆心角之比为2：1，由周角为360°求出所对圆心角∠AOB的度数，即为弦所对圆心角的度数．
解答：解：根据题意画出图形为：

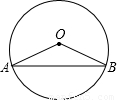
∵弦AB把⊙O分成1：2两部分，
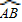
∴的度数为：360×=120°，
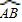
又所对的圆心角为∠AOB，
∴∠AOB=120°．
故答案为：120
点评：此题考查了圆心角，弧及弦之间的关系，其关系可简化为：等弦对等弧（分优弧和劣弧），等角对等弧，等弧等对弦，等弧对等角，等角对等弦，等弦对等角，熟练掌握这些关系是解本题的关键．