
【题目】已知:如图,在△ABC中,点D、E分别在边BC和AB上,且AD=AC,EB=ED,分别延长ED、AC交于点F.

(1)求证:△ABD∽△FDC;
(2)求证:AE2=BEEF.
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
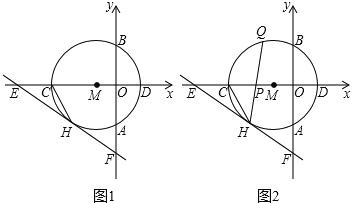
【题目】如图1所示,以点M(1,0)为圆心的圆与y轴,x轴分别交于点A,B,C,D,与⊙M相切于点H的直线EF交x轴于点E(![]() ,0),交y轴于点F(0,
,0),交y轴于点F(0,![]() ).
).
(1)求⊙M的半径r;
(2)如图2所示,连接CH,弦HQ交x轴于点P,若cos∠QHC=![]() ,求
,求![]() 的值;
的值;
(3)如图3所示,点P为⊙M上的一个动点,连接PE,PF,求PF+![]() PE的最小值.
PE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
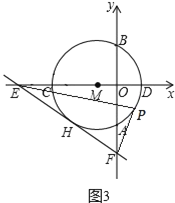
【题目】如图,在平面直角坐标系xOy中,直线![]() 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线![]() 的一个交点为B(-1,4).
的一个交点为B(-1,4).
(1)求直线与双曲线的表达式;
(2)过点B作BC⊥x轴于点C,若点P在双曲线![]() 上,且△PAC的面积为4,求点P的坐标.
上,且△PAC的面积为4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点P为AD上一个动点,以PB 为对称轴将△APB折叠得到△EPB,点A的对称点为点E,射线BE交矩形ABCD的边于点 F,若AB=4,AD=6,当点F为矩形ABCD边的中点时,AP的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
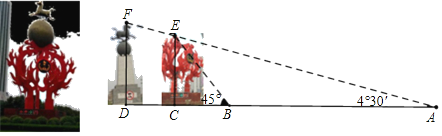
【题目】“马踏飞燕”作为商丘的地标性雕塑被拆分为两座雕塑,安放在紧邻高速公路出站口的平原路和华商大道交叉口,不光临近古城景区,也靠近火神台,恰恰实现了商丘市的城市文化宣传的目的.“人们来到商丘,一下高速,就看到商丘的地标,就能够感受到商丘的火文化.”
某中学数学兴趣小组准备测量安放后的雕塑相关数据,如图,小明从A点测得“火球”最高点E的仰角为4°30′,此处恰好看不到“马踏飞燕”雕塑的最高点F,小明向雕塑走140m到达点B,此时测得点E的仰角为45°.已知两雕塑的距离为50m,求两座雕塑EC、FD的高度.(A、B、C、D在同一直线上)(精确到1m,参考值:sin4°30′≈0.07,cos4°30′≈0.99,tan4°30′≈0.08.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活质量的提高,人们健康意识逐渐增强,安装净水设备的百姓家庭越来越多.某厂家从去年开始投入生产净水器,生产净水器的总量y(台)与今年的生产天数x(天)的关系如图所示.今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.
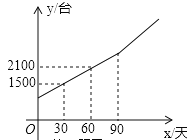
(1)求y与x之间的函数表达式;
(2)已知该厂家去年平均每天的生产数量与今年前90天平均每天的生产数量相同,求厂家去年生产的天数;
(3)如果厂家制定总量不少于6000台的生产计划,那么在改进技术后,至少还要多少天完成生产计划?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区调查社区居民双休日的学习状况,采取下列调查方式:①从一幢高层住宅楼中选取200名居民;②从不同住层楼中随机选取200名居民;③选取社区内的200名在校学生.
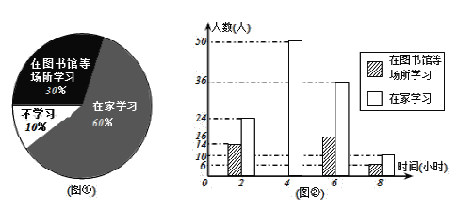
(1)上述调查方式最合理的是 (填序号);
(2)将最合理的调查方式得到的数据制成扇形统计图(如图①)和频数分布直方图(如图②).
①请补全直方图(直接画在图②中);
②在这次调查中,200名居民中,在家学习的有 人;
(3)请估计该社区2000名居民中双休日学习时间不少于4h的人数;
(4)小明的叔叔住在该社区,那么双休日他去叔叔家时,正好叔叔没有学习的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-2![]() mx+m2+m-1(m为常数).
mx+m2+m-1(m为常数).
(1)求证:不论m为何值,该二次函数的图像与x轴总有两个公共点;
(2)将该二次函数的图像向下平移k(k>0)个单位长度,使得平移后的图像经过点(0,-2),则k的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴,y轴分别交于点A(2,0),点B(0,2![]() ),动点D以1个单位长度/秒的速度从点A出发向x轴负半轴运动,同时动点E以
),动点D以1个单位长度/秒的速度从点A出发向x轴负半轴运动,同时动点E以![]() 个单位长度/秒的速度从点B出发向y轴负半轴运动,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F
个单位长度/秒的速度从点B出发向y轴负半轴运动,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F
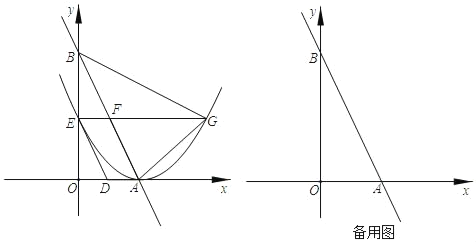
(1)求∠OAB度数;
(2)当t为何值时,四边形ADEF为菱形,请求出此时二次函数解析式;
(3)是否存在实数t,使△AGF为直角三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com