
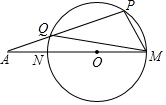
 如图,MN是⊙O的直径,∠A=20°,∠PMQ=50°,以PM为边作圆的内接正多边形,则这个正多边形是( )
如图,MN是⊙O的直径,∠A=20°,∠PMQ=50°,以PM为边作圆的内接正多边形,则这个正多边形是( )| A. | 正七边形 | B. | 正八边形 | C. | 正六边形 | D. | 正十边形 |
分析 首先根据圆周角定理得出∠POQ=100°,进而利用等腰三角形的性质得出∠OPQ=∠OQP,再由外角的性质得出∠A+∠APO=∠POM=20°+40°=60°,即可得出△POM是等边三角形,再由正六边形的性质得出答案.
解答 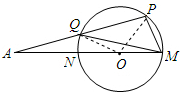 解:连接QO,PO,如图所示;
解:连接QO,PO,如图所示;
∵QO=PO,
∴∠OPQ=∠OQP,
∵∠PMQ=50°,
∴∠POQ=100°,
∴∠OPQ+∠OQP=180°-100°=80°,
∴∠OPQ=∠OQP=40°,
∴∠A+∠APO=∠POM=20°+40°=60°,
∵PO=OM,
∴△POM是等边三角形,
∴PM=OP=OM,
∴以PM为边作圆的内接正多边形,则这个正多边形是正六边形.
故选C.
点评 此题主要考查了正六边形的性质以及圆周角定理和外角的性质等知识,根据已知得出△POM是等边三角形是解题关键.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
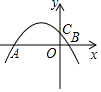 如图,抛物线y=-x2+bx+c的图象与x轴交于A、B两点,与y轴相交于点C,如果OB=OC=$\frac{1}{2}$OA,那么b的值为( )
如图,抛物线y=-x2+bx+c的图象与x轴交于A、B两点,与y轴相交于点C,如果OB=OC=$\frac{1}{2}$OA,那么b的值为( )| A. | -2 | B. | -1 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
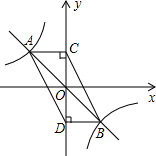 如图,函数y=-x与函数y=-$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为( )
如图,函数y=-x与函数y=-$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为( )| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
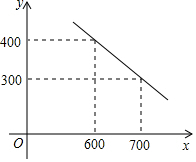 某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,也不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似于一次函数y=kx+b的关系,如图所示.
某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,也不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似于一次函数y=kx+b的关系,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
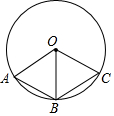 如图,OA,OB,OC是⊙O的三条半径.
如图,OA,OB,OC是⊙O的三条半径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com