
【题目】如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是过
是过![]() 点的一条直线,且
点的一条直线,且![]() 、
、![]() 在
在![]() 的异侧,
的异侧,![]() 于
于![]() ,
,![]() 于
于![]() .
.
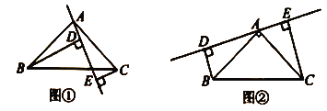
(1)求证:![]() .
.
(2)若将直线![]() 绕点
绕点![]() 旋转到图②的位置时(
旋转到图②的位置时(![]() ),其余条件不变,问
),其余条件不变,问![]() 与
与![]() 、
、![]() 的关系如何?请予以证明.
的关系如何?请予以证明.
【答案】(1)见解析;(2)BD=DE-CE,理由见解析.
【解析】
(1)根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE,AD=CE,因为AE=AD+DE,所以BD=DE+CE;
(2)根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE,AD=CE,因为AD+AE=BD+CE,所以BD=DE-CE.
解:(1)∵∠BAC=90°,BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∵∠ABD+∠BAE=90°,∠CAE+∠BAE=90°
∴∠ABD=∠CAE,
∵AB=AC,
在△ABD和△CAE中,
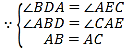
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE=AD+DE,
∴BD=DE+CE;
(2)![]() 与
与![]() 、
、![]() 的数量关系是BD=DE-CE,理由如下:
的数量关系是BD=DE-CE,理由如下:
∵∠BAC=90°,BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∴∠ABD+∠DAB=∠DAB+∠CAE,
∴∠ABD=∠CAE,
∵AB=AC,
在△ABD和△CAE中,
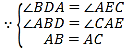
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∴AD+AE=BD+CE,
∵DE=BD+CE,
∴BD=DE-CE.


科目:初中数学 来源: 题型:
【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数![]() 与
与![]() 满足
满足![]() ,
,![]() ,
,![]() ,则称这两个函数互为“旋转函数”.
,则称这两个函数互为“旋转函数”.
求函数![]() 的“旋转函数”.
的“旋转函数”.
小明是这样思考的:由函数![]() 可知,
可知,![]() ,
,![]() ,
,![]() ,根据
,根据![]() ,
,![]() ,
,![]() ,求出
,求出![]() ,
,![]() ,
,![]() ,就能确定这个函数的“旋转函数”.
,就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面问题:
(1)直接写出函数![]() 的“旋转函数”;
的“旋转函数”;
(2)若函数![]() 与
与![]() 互为“旋转函数”,求
互为“旋转函数”,求![]() 的值;
的值;
(3)已知函数![]() 的图象与
的图象与![]() 轴交于点A、B两点(A在B的左边),与
轴交于点A、B两点(A在B的左边),与![]() 轴交于点C,点A、B、C关于原点的对称点分别是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数
轴交于点C,点A、B、C关于原点的对称点分别是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数![]() 互为“旋转函数”。
互为“旋转函数”。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农八师石河子市某中学初三(1)班的学生,在一次数学活动课中,来到市游憩广场,测量坐落在广场中心的王震将军的铜像高度,已知铜像底座的高为3.5m.某小组的实习报告如下.请你计算出铜像的高(结果精确到0.1m)
实习报告2003年9月25日
题目1 | 测量底部可以到达的铜像高 | |||
| ||||
测 得 数 据 | 测量项目 | 第一次 | 第二次 | 平均值 |
BD的长 | 12.3m | 11.7m | ||
测倾器CD的高 | 1.32m | 1.28m | ||
倾斜角 | α=30°56' | α=31°4' | ||
计 算 | ||||
结果 | ||||
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )

A. 30° B. 35° C. 40° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援困山区,某学校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品与用120元购买A型学习用品的件数相同.
(1)求A,B两种学习用品的单价各是多少元;
(2)若购买A、B两种学习用品共1000件,且总费用不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() 于点
于点![]() .
.
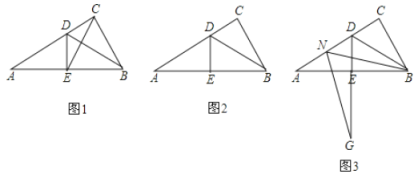
(1)如图![]() ,连接
,连接![]() ,求证:
,求证:![]() 是等边三角形;
是等边三角形;
(2)点![]() 是线段
是线段![]() 上的一点(不与点
上的一点(不与点![]() 重合),以
重合),以![]() 为一边,在
为一边,在![]() 的下方作
的下方作![]() ,
,![]() 交
交![]() 延长线于点
延长线于点![]() ,请你在图
,请你在图![]() 中画出完整图形,并直接写出
中画出完整图形,并直接写出![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(3)如图![]() ,点
,点![]() 是线段
是线段![]() 上的一点,以
上的一点,以![]() 为一边,在
为一边,在![]() 的下方作
的下方作![]() ,
,![]() 交
交![]() 延长线于点
延长线于点![]() ,试探究
,试探究![]() 与
与![]() 数量之间的关系,并说明理由.
数量之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
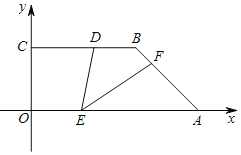
【题目】如图,BC⊥y轴,BC<OA,点A,点C分别在x轴、y轴的正半轴上,D是线段BC上一点,BD=![]() OA=
OA=![]() ,AB=3,∠OAB=45°,E,F分别是线段OA,AB上的两动点,且始终保持∠DEF=45°.将△AEF沿一条边翻折,翻折前后两个三角形组成的四边形为菱形,则线段OE的值为______.
,AB=3,∠OAB=45°,E,F分别是线段OA,AB上的两动点,且始终保持∠DEF=45°.将△AEF沿一条边翻折,翻折前后两个三角形组成的四边形为菱形,则线段OE的值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com