
 我们把:“有一组邻角相等的凸四边形”叫做“等邻角四边形”.
我们把:“有一组邻角相等的凸四边形”叫做“等邻角四边形”.分析 (1)根据等邻边四边形的定义即可,
(2)①作出辅助线,判断出△DFA≌△CEB,再判断出四边形DFEC是平行四边形,即可;②举出反例来说明;
(3)分四种情况画图计算即可.
解答 解(1)矩形,
∵矩形的四个角都是直角,
根据“等邻角四边形”的定义,
得到矩形是“等邻角四边形”;
(2)①如图,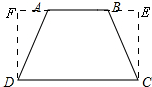
过点C作CE⊥AB,DF⊥AB,
∵∠DAB=∠CBA,
∴∠DAF=∠CBE,
∵CE⊥AB,DF⊥AB,
∴∠DFA=∠CEB=90°,
∵AD=BC,
∴△DFA≌△CEB,
∴DF=CE,
∵∠DFA=∠CEB=90°,
∴DF=EC,
∴四边形DFEC是平行四边形,
∴AB∥CD;
②假命题,
反例如图,
在等腰三角形的腰上取点D,E,使得DE=BC,四边形DBCE是等邻边四边形,没有对边平行.
(3)①∠D=∠A=90°,
如图,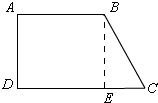
作BE⊥DC,
∵∠D=∠A=∠BED=90°,
∴四边形ADEB是矩形,
∴DE=AB=6.
在Rt△BEC中,BC=10,∠C=60°,
∴CE=5,
∴CD=DE+CE=11,
②如图,∠A=∠B=90°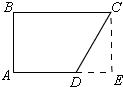
作CE⊥AD,
∵∠A=∠B=∠AEC=90°,
∴四边形ABCE是矩形,
∴AE=BC=10,CE=AB=6,
在Rt△CED中,∠DCE=∠BCE-∠BCD=30°,
∴CD=4$\sqrt{3}$,
③∠B=∠C=60°.
如图,延长AD,BC交于E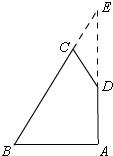
在Rt△ABE中,∠B=60°,AB=6,
∴BE=2AB=12,∠E=30°
∴CE=BE-BC=12-10=2,
∵∠BCD=60°,
∴∠CDE=∠CED=30°,
∴CD=CE=2,
④∠D=∠C=60°,
如图,延长DA,CB交于E,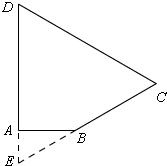
∵∠D=∠C=60°,
∴∠E=60°,CD=CE,
在Rt△ABE中,∠E=60°,AB=6,
∴BE=4$\sqrt{3}$,
∴CD=BC+BE=10+4$\sqrt{3}$.
点评 此题是四边形综合题,主要考查了平行四边形的判定和性质,矩形的判定和性质,直角三角形的性质,全等三角形的判定和性质,解本题的关键是作出图形,也是本题的难点.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
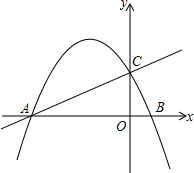 如图,已知直线y=$\frac{2}{5}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+4ax+b经过A、C两点,与x轴交于另-点B.
如图,已知直线y=$\frac{2}{5}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+4ax+b经过A、C两点,与x轴交于另-点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{x}^{2}+{y}^{2}}$=$\sqrt{{x}^{2}}$+$\sqrt{{y}^{2}}$ | B. | $\sqrt{x-y}$=$\sqrt{x}$-$\sqrt{y}$ | C. | 5$\sqrt{7}$-3$\sqrt{5}$=2$\sqrt{2}$ | D. | 4$\sqrt{5}$-3$\sqrt{5}$=$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有最大值-1 | B. | 有最小值-1 | C. | 有最大值1 | D. | 有最小值1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com