
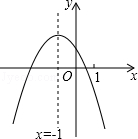
 二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论:| A、4个 | B、3个 | C、2个 | D、1个 |
| b |
| 2a |
| b |
| 2 |
| b |
| 2 |
| b |
| 2a |
| b |
| 2 |
| b |
| 2 |


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
| A、y1<y2<y3 |
| B、y3<y2<y1 |
| C、y2<y1<y3 |
| D、y2<y3<y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
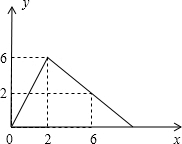 某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后:
某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com