
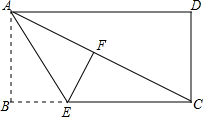
 已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )
已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 在Rt△ABC中利用勾股定理可求出AC=10,设BE=a,则CE=8-a,根据折叠的性质可得出BE=FE=a,AF=AB=6,∠AFE=∠B=90°,进而可得出FC=4,在Rt△CEF中,利用勾股定理可得出关于a的一元二次方程,解之即可得出a值,将其代入8-a中即可得出线段CE的长度.
解答 解:在Rt△ABC中,AB=6,BC=8,
∴AC=10.
设BE=a,则CE=8-a,
根据翻折的性质可知,BE=FE=a,AF=AB=6,∠AFE=∠B=90°,
∴FC=4.
在Rt△CEF中,EF=a,CE=8-a,CF=4,
∴CE2=EF2+CF2,即(8-a)2=a2+42,
解得:a=3,
∴8-a=5.
故选C.
点评 本题考查了翻折变换、矩形的性质、勾股定理以及解一元二次方程,在Rt△CEF中,利用勾股定理找出关于a的一元二次方程是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 对某班学生体重情况的调查 | |
| B. | 对某办公室职员年龄的调查 | |
| C. | 对某班学生每天课余工作时间的调查 | |
| D. | 对某批次汽车的抗撞击能力的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
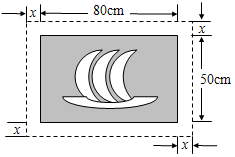 如图所示,在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整幅挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
如图所示,在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图.如果要使整幅挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )| A. | x2+130x-1400=0 | B. | x2+65x-350=0 | C. | x2-130x-1400=0 | D. | x2-65x-350=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
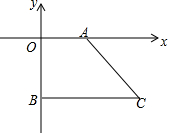 如图,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于点B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16,求C点坐标.
如图,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于点B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16,求C点坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com