【题目】为了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查．已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制成如下统计图表(单位：cm)：
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
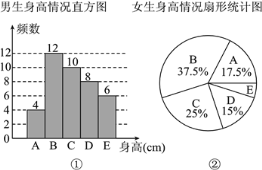
根据图表提供的信息，样本中，身高在160≤x＜170之间的女生人数为( )
A. 8 B. 6 C. 14 D. 16
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目：初中数学 来源： 题型：
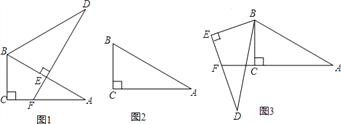
【题目】将两个全等的直角三角形ABC和DBE按图①方式摆放，其中∠ACB=∠DEB=90°，∠A=∠D=30°，点E落在AB上，DE所在直线交AC所在直线于点F．
（1）求证：AF+EF=DE；
（2）若将图①中的△DBE绕点B按顺时针方向旋转角α，且0°＜α＜60°，其它条件不变，请在图②中画出变换后的图形，并直接写出你在（1）中猜想的结论是否仍然成立；
（3）若将图①中的△DBE绕点B按顺时针方向旋转角β，且60°＜β＜180°，其它条件不变，如图③．你认为（1）中猜想的结论还成立吗？若成立，写出证明过程；若不成立，请写出AF、EF与DE之间的关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
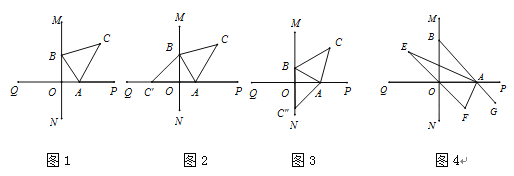
【题目】直线MN与直线PQ垂直相交于O，点A在射线OP上运动，点B在射线OM上运动，连接AB．
（1）如图，已知AC、BC分别是∠BAP和∠ABM角的平分线，
①点A、B在运动的过程中，∠ACB的大小是否发生变化？若发生变化，请说明理由；若不发生变化，试求出∠ACB的大小．
②如图，将△ABC沿直线AB折叠，若点C落在直线PQ上，记作点C′，则∠ABO＝ °；如图，将△ABC沿直线AB折叠，若点C落在直线MN上，记作点C′′，则∠ABO＝ °．
（2）如图，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线交于E、F，在△AEF中，如果有一个角是另一个角的
倍，求∠ABO的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
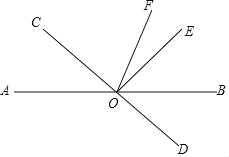
【题目】如图，直线AB，CD交于点O，OB平分∠DOE，OF是∠BOC的角平分线．
(1)说明：∠AOC＝∠BOE；
(2)若∠AOC＝46°，求∠EOF的度数；
(3)若∠EOF＝30°，求∠AOC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
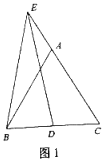
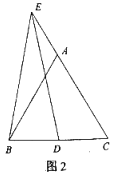
【题目】如图1，△ABC是等边三角形，点D是BC上一点，点E在CA的延长线上，连结EB、ED，且EB=ED.
(1)求证:∠DEC=∠ABE；
(2)点D关于直线EC的对称点为M,连接EM、BM：
①依题意将图2补全；
②求证:EB=BM.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在⊙O中，半径OA⊥OB，过点OA的中点C作FD∥OB交⊙O于D、F两点，且CD= 
，以O为圆心，OC为半径作 
，交OB于E点．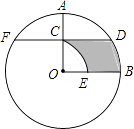
（1）求⊙O的半径OA的长；
（2）计算阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
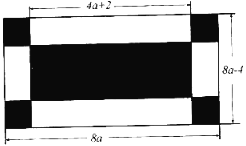
【题目】如图,某小区有一块长为
米、宽为
米的长方形地块该长方形地块。该长方形地块正中间是一个长为
米的长方形,四个角是大小相同的正方形,该小区计划
将如图阴影部分进行绿化,对四个角的四个正方形采用A绿化方案,对正中间的长方形采用B绿化方案.
(1)采用A绿化方案的每个正方形边长是多少米，采用B绿化方案的长方形另一边长是多少米(用含
的代数式表示)；
(2)若采用A、B两种绿化方案的总造价相同,均为2700元,请你判断哪种方案单位面积造价高?并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y=x+1与x轴交于点A，与y轴交于点B，△BOC与△B′O′C′是以点A为位似中心的位似图形，且相似比为1：3，则点B的对应点B′的坐标为 ．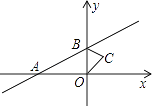 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某八年级计划用360元购买笔记本奖励优秀学生，在购买时发现，每本笔记本可以打九折，结果买得的笔记本比打折前多10本．
（1）请利用分式方程求出每本笔记本的原来标价；
（2）恰逢文具店周年志庆，每本笔记本可以按原价打8折，这样该校最多可购入本笔记本？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
