
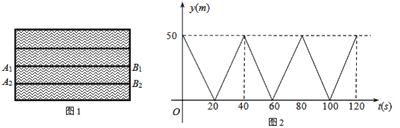
【题目】如图1,A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以2m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图2所示.
(1)赛道的长度是 m,甲的速度是 m/s;
(2)经过多少秒时,甲、乙两人第二次相遇?
(3)若从甲、乙两人同时开始出发到2分钟为止,甲、乙共相遇了 次.2分钟时,乙距池边B1B2的距离为多少米。
【答案】(1)50,2.5;(2)![]() ;(3)5,40米.
;(3)5,40米.
【解析】试题(1)由函数图象可以直接得出赛道的长度为50米,由路程÷时间=速度就可以求出甲的速度.
(2)设经过x秒时,甲、乙两人第二次相遇,根据甲游过的路程+乙游过的路程=150米建立方程求出其解即可;
(3)分别求出相遇一次的时间就可以求出相遇次数,再由速度与时间的关系就可以求出结论.
试题解析:(1)由图象,得
赛道的长度是:50米,
甲的速度是:50÷20=2.5m/s.
(2)设经过x秒时,甲、乙两人第二次相遇,由题意,得
2.5x+2x=150,
解得:x=![]() ;
;
(3)由题意可以得出第一次相遇的时间为: ![]() ,
,
第二次相遇的时间为: ![]() ,
,
第三次相遇的时间为: ![]() ,
,
第四次相遇的时间为: ![]() ,
,
第五次相遇的时间为: ![]() ,
,
第六次相遇的时间为: ![]() >120s,
>120s,
∴甲、乙共相遇5次.
2分钟时,乙距池边B1B2的距离为:2×(120-100)=40米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的![]() .
.
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)(﹣1)2018+3﹣2﹣(π﹣3.14)0
(2)(x+3)2﹣x2
(3)(x+2)(3x﹣y)﹣3x(x+y)
(4)(2x+y+1)(2x+y﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影 A, B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为 y (cm).

(1)填空:从图可知,每个小长方形较长的一边长是_________cm (用含y的代数式表示).
(2)分别求出阴影 A,B的面积,并计算阴影 A,B的面积差?(用含x,y的式子表示)
(3)当y=10时,阴影 A与阴影 B的面积差会随着x的变化而变化吗?请你作出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列各组条件中,不能说明![]() 的是( )
的是( )
A.AB=DE,∠B=∠E,∠C=∠FB.AB=DE,∠A=∠D,∠B=∠E
C.AC=DF,BC=EF,∠A=∠DD.AB=DE,BC=EF,AC=ED
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.
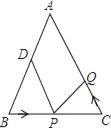
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
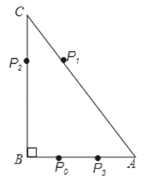
【题目】如图,Rt△ABC中,∠B=90 , BC=12,tanC=![]() . 如果一质点P开始时在AB边的P0处,BP0=3.P第一步从P0跳到AC边的P1(第1次落点)处,且
. 如果一质点P开始时在AB边的P0处,BP0=3.P第一步从P0跳到AC边的P1(第1次落点)处,且![]() ;第二步从P1跳到BC边的P2(第2次落点)处,且
;第二步从P1跳到BC边的P2(第2次落点)处,且![]() ;第三步从P2跳到AB边的P3(第3次落点)处,且
;第三步从P2跳到AB边的P3(第3次落点)处,且![]() ;…;质点P按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2014与点P2015之间的距离为( )
;…;质点P按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2014与点P2015之间的距离为( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O是坐标原点,点A、B分别在y轴的正半轴和x轴的正半轴上,OA=OB,△AOB的面积为18.过点A作直线l⊥y轴.
(1)求点A的坐标;
(2)点C是第一象限直线l上一动点,连接BC,过点B作BD⊥BC,交y轴于点设点D的纵坐标为t,点C的横坐标为d,求t与d的关系式;
(3)在(2)的条件下,过点D作直线DF∥AB,交x轴于点F,交直线l于点E,OF=![]() EC时,求点E的坐标.
EC时,求点E的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com