
分析 (1)根据拆项法,可得答案;
(2)根据拆项法,可得规律;
(3)根据规律,可得答案.
解答 解:(1)$\frac{1}{42}$=$\frac{1}{6×7}$=$\frac{1}{6}$-$\frac{1}{7}$,
故答案为:$\frac{1}{6}$-$\frac{1}{7}$,
(2)规律:$\frac{1}{{n}^{2}+n}$$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(3)原式=$\frac{1}{x+1}$-$\frac{1}{x+2}$+$\frac{1}{x+2}$-$\frac{1}{x+3}$+…+$\frac{1}{x+99}$-$\frac{1}{x+100}$
=$\frac{1}{x+1}$-$\frac{1}{x+100}$
=$\frac{99}{(x+1)(x+100)}$.
点评 本题考查了分式的加减,利用拆项法得出相反数的项是解题关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
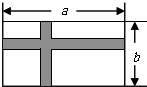 如图,有一块长为a米、宽为b米的长方形空地,现计划在这块空地中间修出两条互相垂直的宽均为2米的道路(图中阴影部分),其余部分进行绿化.
如图,有一块长为a米、宽为b米的长方形空地,现计划在这块空地中间修出两条互相垂直的宽均为2米的道路(图中阴影部分),其余部分进行绿化.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,△AOB的顶点均在边长为1的正方形在顶点上.
如图,平面直角坐标系中,△AOB的顶点均在边长为1的正方形在顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,E,F分别是正方形ABCD中BC和CD边上的点,且AB=4,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF,AE,求证:∠AFE=90°.
如图,E,F分别是正方形ABCD中BC和CD边上的点,且AB=4,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF,AE,求证:∠AFE=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com