
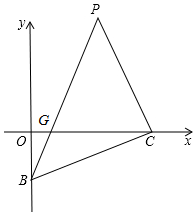
 ��ͼ����D��m��n������m2-6m+$\sqrt{m+n-6}$=-9��BΪy�Ḻ������һ���㣬��DBC=45�㣬BC��x����C��CP��BC��BD�ӳ�����P����x���ڵ�G��
��ͼ����D��m��n������m2-6m+$\sqrt{m+n-6}$=-9��BΪy�Ḻ������һ���㣬��DBC=45�㣬BC��x����C��CP��BC��BD�ӳ�����P����x���ڵ�G������ ��1��������m2-6m+9+$\sqrt{m+n-6}$=0������m-3��2+$\sqrt{m+n-6}$=0�����ݷǸ��������ʼ��ɽ�����⣮
��2����ͼ1�У���D��DN��x����N����DM��y����M������OD����֤���ı���DMON�������Σ��Ƴ���DGO�ס�CGB����$\frac{DG}{CG}$=$\frac{OG}{BG}$���Ƴ�$\frac{DG}{OG}$=$\frac{CG}{BG}$���֡�BOG=��CGD���Ƴ���BGO�ס�CGD���õ���BOG=��CDG=90�㣬�ɴ˼���֤����
��3�����ۣ�$\frac{BM}{CE}$�Ƕ�ֵ��$\frac{BM}{CE}$=1��ֻҪ֤����BQM�ա�CKE���Ƴ�BM=CE�����ɽ�����⣮
��� �⣺��1��������m2-6m+9+$\sqrt{m+n-6}$=0������m-3��2+$\sqrt{m+n-6}$=0��
��m=3��n=3��
���D������3��3����
��2����ͼ1�У���D��DN��x����N����DM��y����M������OD��
��DMO=��DNO=��MON=90�㣬
���ı���DMON�Ǿ��Σ�
��DM=DN=3��
���ı���DMON�������Σ�
���DOG=��GBC=45�㣬�ߡ�DGO=��BGC��
���DGO�ס�CGB��
��$\frac{DG}{CG}$=$\frac{OG}{BG}$��
��$\frac{DG}{OG}$=$\frac{CG}{BG}$���֡ߡ�BOG=��CGD��
���BGO�ס�CGD��
���BOG=��CDG=90�㣬
��CD��PB��
�ߡ�BCP=90�㣬��CBP=��CPB=45�㣬
��CB=CP��
��BD=DP����D���߶�BP�е㣮
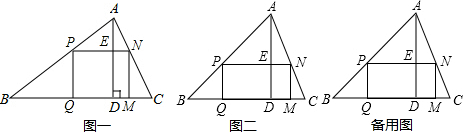
��3�����ۣ�$\frac{BM}{CE}$�Ƕ�ֵ��$\frac{BM}{CE}$=1���������£�
��ͼ2�У���PE��OC��K��
�ڡ�BCF�͡�PCE�У�
$\left\{\begin{array}{l}{BC=PC}\\{��BCF=��PCE}\\{CF=CE}\end{array}\right.$��
���BCF�ա�PCE��
���CBF=��CPE���ߡ�CBP=��CPB��
���MBF=��EPB��
��OB��PE��
���OBG=��EPB=��GBM��
�ߡ�BCO+��PCK=90�㣬��PCK+��CPK=90�㣬
���BCO=��CPK��
�ڡ�BOC�͡�CKP�У�
$\left\{\begin{array}{l}{BC=PC}\\{��BOC=��PKC=90��}\\{��BCO=��CPK}\end{array}\right.$��
���BOC�ա�CKP��
��OB=KC��
�ڡ�BGO�͡�BGQ�У�
$\left\{\begin{array}{l}{BG=BG}\\{��GBO=��GBQ}\\{��BOG=��BQG=90��}\end{array}\right.$��
���BGO�ա�BGQ��
��BO=BQ=CK��
�ڡ�BQM�͡�CKE�У�
$\left\{\begin{array}{l}{��MBQ=��KCE}\\{BQ=CK}\\{��BQM=��CKE=90��}\end{array}\right.$��
���BQM�ա�CKE��
��BM=CE��
��$\frac{BM}{CE}$=1��
���� ���⿼��ȫ�������ε��ж������ʡ����������ε��ж������ʡ�����ֱ�������ε����ʡ��Ǹ��������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ��ѧ�����Ӹ����ߣ��������õ�ȫ�������ε��ж������ڿ�֪ѹ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �����ܴ��� | 500 | 1000 | 1500 | 2000 | 2500 | 3000 | 3500 |
| ����2���˵�������ͬ���Ĵ��� | 480 | 900 | 1320 | 1920 | 2350 | 2910 | 3400 |
| ����2���˵�������ͬ����Ƶ�� | 0.96 | 0.90 | 0.88 | 0.96 | 0.94 | 0.97 | 0.97 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
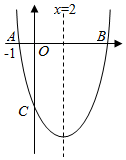 ��ͼ���Գ���Ϊֱ��x=2��������y=x2+bx+c��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C���ҵ�A������Ϊ��-1��0��
��ͼ���Գ���Ϊֱ��x=2��������y=x2+bx+c��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C���ҵ�A������Ϊ��-1��0���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
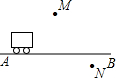 ��ͼ��һ��������ֱ����·AB����A��B��ʻ��M��N�ֱ���λ�ڹ�·����Ĵ�ׯ��
��ͼ��һ��������ֱ����·AB����A��B��ʻ��M��N�ֱ���λ�ڹ�·����Ĵ�ׯ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com