
【题目】已知两个分别含有30°,45°角的一副直角三角板.
(1)如图1叠放在一起
若OC恰好平分∠AOB,则∠AOD= 度;
若∠AOC=40°,则∠BOD= 度;
(2)如图2叠放在一起,∠AOD=4∠BOC,试计算∠AOC的度数.

【答案】(1)135,40;(2)∠AOC的度数为110°.
【解析】
(1)①根据角平分线的定义求出∠AOC,再根据∠AOD=∠AOC+∠COD代入数据进行计算即可得解;
②由已知可求得∠BOC,再根据∠BOD=∠COD-∠BOC代入数据进行计算即可得解;
(2)由已知可求得∠BOD,再根据∠AOC=∠AOB+∠COD-∠BOD代入数据进行计算即可得解.
(1)①∵OC平分∠AOB,∠AOB=90°,
∴∠AOC=![]() ∠AOB=45°,
∠AOB=45°,
∴∠AOD=∠AOC+∠COD=45°+90°=135°;
②由已知∠BOC=90°-∠40°=50°,
∴∠BOD=∠COD-∠BOC=90°-50°=40°,
故答案为:135,40
(2)∵∠AOD=4∠BOC,
∴∠AOB-∠BOD=4(∠COD-∠BOD),
即90°-∠BOD=4(-30°∠BOD),解得:∠BOD=10°,
∴∠AOC=∠AOB+∠COD-∠BOD=90°+30°-10°=110°
即∠AOC的度数为110°.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与x轴、y轴分别交于A、B两点且与反比例函数
的图象与x轴、y轴分别交于A、B两点且与反比例函数![]() 的图象在第一象限交于C点,CD⊥
的图象在第一象限交于C点,CD⊥![]() 轴于D点,若∠CAD=
轴于D点,若∠CAD=![]() ,AB =
,AB =![]() ,CD =
,CD =![]()
(1)求点A、B、D的坐标;
(2)求一次函数的解析式;
(3)反比例函数的解析式;
(4)求△BCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四点A,B,C,D,用圆规和无刻度的直尺按下列要求与步骤画出图形并计算:

(1)画直线AB;
(2)画射线DC;
(3)延长线段DA至点E,使AE=AB;(保留作图痕迹)
(4)画一点P,使点P既在直线AB上,又在线段CE上;
(5)若AB=2cm,AD=1cm,求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距80km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论,正确的个数是( )
①甲骑车速度为30km/小时,乙的速度为20km/小时;
②l1的函数表达式为y=80﹣30x;
③l2的函数表达式为y=20x;
④![]() 小时后两人相遇.
小时后两人相遇.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
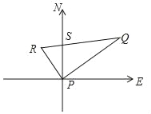
【题目】如图,某港口P位于东西方向的海岸线上,A、B两艘轮船同时从港口P出发,各自沿一固定方向航行,A轮船每小时航行12海里,B轮船每小时航行16海里.它们离开港口一个半小时后分别位于点R、Q处,且相距30海里.已知B轮船沿北偏东60°方向航行.
(1)A轮船沿哪个方向航行?请说明理由;
(2)请求出此时A轮船到海岸线的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形 ABCD 中,点 E 是对角线 BD 上一动点,AE 的延长线交 CD 于点 F,交 BC 的延长线于点 G,M 是 FG 的中点.
(1)求证: ∠DAE=∠DCE;
(2)判断线段 CE 与 CM 的位置关系,并证明你的结论;
(3)当![]() ,并且
,并且![]() 恰好是等腰三角形时,求 DE 的长.
恰好是等腰三角形时,求 DE 的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com