练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    23、下列为边长为1的小正方形组成的网格图．
    ①请画出△ABC关于直线a对称的图形（不要求写作法）；
    ②求△ABC的面积（直接写出即可）．
    分析：（1）从三角形各边向a引垂线并延长相同的长度，找到对应点，顺次连接．
    （2）利用网格求三角形的面积，让矩形的面积-三个三角形的面积．
    解答：解：（1）如图：

    （2）S△ABC=矩形的面积-三个三角形的面积
    =3×4-3×1÷2-3×2÷2-4×1÷2=5.5．（4分）
    点评：考查的是作简单平面图形轴对称后的图形，及利用网格求图形的面积的能力．作此题时，三角形的底和高都不太好计算，可以利用图中图形的面积关系计算．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2013•太原二模）下列各图中的六边形都是边长为1的正六边形，点O是其对角线的交点，请在正六边形内部以它的顶点为圆心，1为半径画弧．

    （1）图1是小颖按要求画出的图形，这个图形是
    轴
    轴
    对称图形；
    （2）请你在图2中按要求添加一些弧线，使整个图形既是轴对称图形也是中心对称图形；
    （3）请你在图3中按要求添加一些弧线，使整个图形是中心对称图形但不是轴对称图形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：013

    如图，每个大正方形均由边长为1的小正 方形组成，则下列图中三角形(阴影部分)与△ABC相似的是(　　)．

    　　　　　

    查看答案和解析>>

    科目：初中数学 来源：新海实验中学2008年中考第一次模拟考试数学试题 题型：044

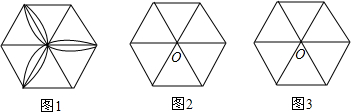
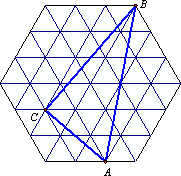
    下面三个图形的外围是正六边形，内部被分割成若干个正三角形的网格图(规定：最小正方形的边长为1)，请你解答下列问题：

    (1)在图(1)中，△ABC是直角三角形吗？说明你的理由．

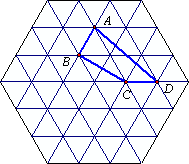
    (2)在图(2)中，把四边形ABCD向下平移个单位、向左平移2个单位，作出平移后的图形A1B1C1D1．再作出把四边形A1B1C1D1绕点A1逆时针旋转60°的图形．四边形A1B1C1D1的面积为________．

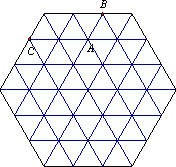
    (3)在图(3)中，A、B、C是网格图的三个格点，请你在网格中找出所有的格点D，使A、B、C、D构成一个轴对称图形；在网格图的外围(最大的正六边形的边上)再找一点E，使△ABC与△ACE相似，且相似比不为1．

    查看答案和解析>>

    科目：初中数学 来源：2013届北京市昌平区九年级上学期期末考试数学试卷（带解析） 题型：解答题

    阅读下面材料：
    小伟遇到这样一个问题：如图1，在正三角形ABC内有一点P，且PA="3" ，PB=4，PC=5，求∠APB的度数.
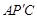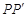    小伟是这样思考的：如图2，利用旋转和全等的知识构造△，连接，得到两个特殊的三角形，从而将问题解决．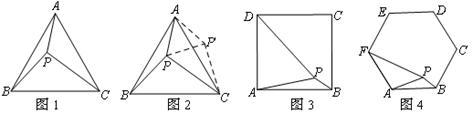

    请你回答：图1中∠APB的度数等于　　   .
    参考小伟同学思考问题的方法，解决下列问题：
    （1）如图3，在正方形ABCD内有一点P，且PA=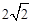，PB=1，PD=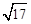，则∠APB的度数等于     ，正方形的边长为     ；
    （2）如图4，在正六边形ABCDEF内有一点P，且PA=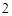，PB=1，PF=，则∠APB的度数等于     ，正六边形的边长为     ．

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年北京市昌平区九年级上学期期末考试数学试卷（解析版） 题型：解答题

    阅读下面材料：

    小伟遇到这样一个问题：如图1，在正三角形ABC内有一点P，且PA="3" ，PB=4，PC=5，求∠APB的度数.

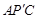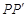    小伟是这样思考的：如图2，利用旋转和全等的知识构造△，连接，得到两个特殊的三角形，从而将问题解决．

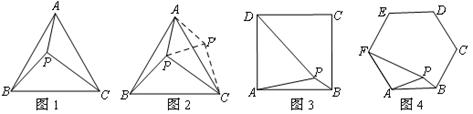
    请你回答：图1中∠APB的度数等于　　   .

    参考小伟同学思考问题的方法，解决下列问题：

    （1）如图3，在正方形ABCD内有一点P，且PA=，PB=1，PD=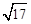，则∠APB的度数等于     ，正方形的边长为     ；

    （2）如图4，在正六边形ABCDEF内有一点P，且PA=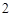，PB=1，PF=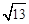，则∠APB的度数等于     ，正六边形的边长为     ．

     

    查看答案和解析>>

    同步练习册答案