

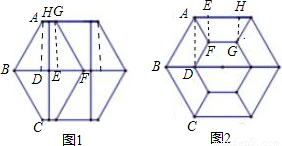
 解:如图1所示,作AD⊥BF,GE⊥BF,设AB=a;
解:如图1所示,作AD⊥BF,GE⊥BF,设AB=a; =120°,∠ABD=
=120°,∠ABD= =60°;
=60°; ,正六边形的对角线长为2a,
,正六边形的对角线长为2a,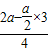 =
=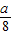 ;
; ,AD=
,AD= ,则EF=
,则EF= AD=
AD=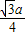 ,
, =60°,∠AFE=30°,
=60°,∠AFE=30°, ×
×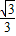 =
=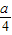 ,
, ×2=
×2=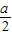 .
.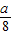 :
: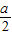 =
= .
.

科目:初中数学 来源: 题型:
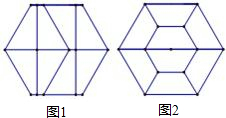 某校九年级学生开展了丰富多彩的数学课题学习活动.在探讨《美丽的正六边形》课题学习时,发现正六边形可以分成八个全等的直角梯形(如图1),也可以分成八个全等的等腰梯形(如图2),则直角梯形的最短边与等腰梯形的最短边的比值是
某校九年级学生开展了丰富多彩的数学课题学习活动.在探讨《美丽的正六边形》课题学习时,发现正六边形可以分成八个全等的直角梯形(如图1),也可以分成八个全等的等腰梯形(如图2),则直角梯形的最短边与等腰梯形的最短边的比值是查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省杭州市翠苑中学九年级(上)月考数学试卷(9月份)(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2012年安徽省合肥市包河区中考数学二模试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2007年浙江省温州市洞头县中考数学二模试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2010年中考数学考前10日信息题复习题精选(5)(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com