
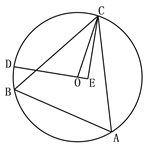
【题目】如图,△ABC为⊙O的内接三角形,BC=24 , ![]() ,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )
,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
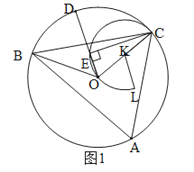
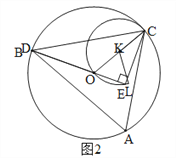
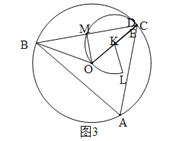
【解析】解:当点D由B点沿弧BC运动到点C时,点E经过的路径是以OC的中点K为圆心,以![]() OC为半径的一段圆弧,圆心角为240°,如图1.当D与B重合时,如图2,E和L重合.∵∠A=60°,∴∠BOC=120°,∴∠COE=60°.∵OK=KL,∴△OKL是等边三角形,∴∠OKL=60°.当D运动到C时,如图3,D、E、C三点重合,此时∠OKC=180°,∴∠LKC=60°+180°=240°.过O作OM⊥BC于M,如图3,则BM=
OC为半径的一段圆弧,圆心角为240°,如图1.当D与B重合时,如图2,E和L重合.∵∠A=60°,∴∠BOC=120°,∴∠COE=60°.∵OK=KL,∴△OKL是等边三角形,∴∠OKL=60°.当D运动到C时,如图3,D、E、C三点重合,此时∠OKC=180°,∴∠LKC=60°+180°=240°.过O作OM⊥BC于M,如图3,则BM=![]() BC=12.∵∠BOC=120°,OB=OC,∴∠MBO=(180°-120°)÷2=30°,∴OM=
BC=12.∵∠BOC=120°,OB=OC,∴∠MBO=(180°-120°)÷2=30°,∴OM=![]() ,OB=2OM=
,OB=2OM=![]() ,∴OK=
,∴OK=![]() OB=
OB=![]() ,∴点E经过的路径长为
,∴点E经过的路径长为![]() =
=![]() .故选C.
.故选C.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
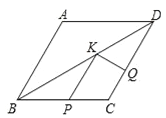
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
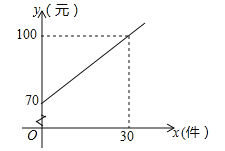
【题目】某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.
(1)求每位“快递小哥”的日收入y(元)与日派送量x(件)之间的函数关系式;
(2)已知某“快递小哥”的日收入不少于110元,则他至少要派送多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
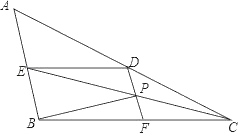
【题目】如图,在△ABC中,CE平分∠ACB交AB于E点,DE∥BC,DF∥AB.
(1)若∠BCE=25°,请求出∠ADE的度数;
(2)已知:BF=2BE,DF交CE于P点,连结BP,AB⊥BP.
①猜想:△CDF的边DF与CD的数量关系,并说明理由;
②取DE的中点N,连结NP.求证:∠ENP=3∠DPN.
查看答案和解析>>
科目:初中数学 来源: 题型:
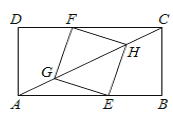
【题目】如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是_________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图所示的图形,回答下列问题:
(1) 图中的点被线段隔开分成四层,第一层有1个点,第二层有3个点,第三层有5个点,第四层有___________个点;
(2) 如果要你继续画下去,那么第五层有________点, 第10层有_________点;
(3) 某一层上有77个点,你可知道这是第_________层;
(4) 第一层与第二层的和是__________,前三层的和是_________,前四层和为____________,
你有没有发现什么规律?
根据你的推测,前一百层的和是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形OABC中,点A的坐标是(﹣3,1),点B的纵坐标是4,则B,C两点的坐标分别是( )
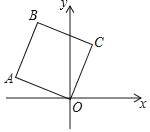
A. (﹣2,4),(1,3) B. (﹣2,4),(2,3)
C. (﹣3,4),(1,4) D. (﹣3,4),(1,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①点G是BC中点;②FG=FC;③与∠AGB相等的角有5个;④S△FGC=![]() .其中正确的是( )
.其中正确的是( )
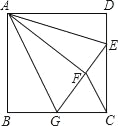
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com