
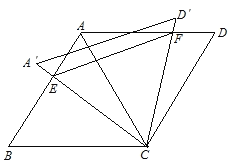
【题目】如图,菱形ABCD中,边长为2,∠B=60°,将△ACD绕点C旋转,当AC(即A′C)与AB交于一点E,CD(即CD′)同时与AD交于一点F时,点E,F和点A构成△AEF。试探究△AEF的周长是否存在最小值,如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.
【答案】2+![]()
【解析】试题分析:根据菱形和旋转的性质,以及∠B=60°,可得△ABC,△ACD和△A′CD′是等边三角形,推出∠BCE=∠ACF,证出△BCE≌△ACF(ASA),得出BE=AF,CE=CF,推出△ECF是等边三角形,根据CF的最小值为点C到AD的距离,即EF的最小值是![]() ,可求出△AEF的周长的最小值.
,可求出△AEF的周长的最小值.
试题解析:△AEF的周长存在最小值。理由如下:
根据菱形和旋转的性质,以及∠B=60°,可得△ABC,△ACD和△A′CD′是等边三角形,
∴∠BCA=∠BCE+∠ACE=60°,∠ECF=∠ACF+∠ACE=60°。
∴∠BCE=∠ACF
在△BCE与△ACF中,
∴△BCE≌△ACF(ASA)
∴BE=AF,CE=CF,AE+AF=AE+BE=AB,
∵∠ECF=60°,
故△ECF是等边三角形,
EF=CF
∵CF的最小值为点C到AD的距离![]() (如图),
(如图),
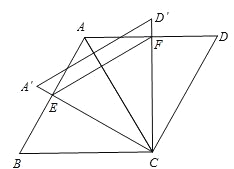
∴EF的最小值是![]() 。
。
∵△AEF的周长=AE+AF+EF=AB+EF,
∴△AEF的周长的最小值为2+![]() 。
。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,ABCD中,对角线AC、BD交于点O,直线EF经过点O,分别交DA,BC的延长线于点E,F,连接BE,DF. 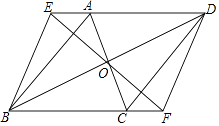
求证:
(1)AE=CF;
(2)四边形BEDF是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有长为3cm,4cm,6cm,8cm的木条各两根,小明与小刚分别取了3cm和4cm的两根,要使两人拿的三根木条组成的两个三角形全等,则他们所取的第三根木应为( )
A. 一人取6cm的木条,一人取8cm的木条 B. 两人都取6cm的木条
C. 两人都取8cm 的木条 D. B、C两种取法都可以
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1 , 如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1 , 使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是 . 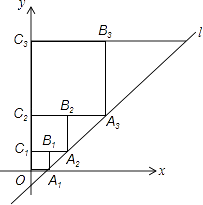
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的三条边的长分别为3、4、5,与△ABC相似的△A′B′C′的最长边为15.则△A′B′C′最短边的长为_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com