
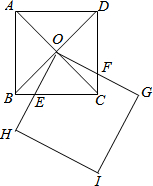
 在边长为2的正方形ABCD中,对角线AC与BD相交于点O,另一个正方形OHIG绕点O旋转(如图),设OH与边BC交于点E(与点B、C不重合),OG与边CD交于点F.
在边长为2的正方形ABCD中,对角线AC与BD相交于点O,另一个正方形OHIG绕点O旋转(如图),设OH与边BC交于点E(与点B、C不重合),OG与边CD交于点F.分析 (1)由四边形ABCD是正方形,得到OB=OC∠BOC=90°,∠OBE=∠OCF=45°,根据四边形OHIG是正方形,得到∠GOH=90°,根据余角的性质得到∠BOE=∠COF,推出△BOE≌△COF(ASA),根据全等三角形的性质即可得到结论;
(2)根据全等三角形的性质得到S四边形OECF=S△BOC,根据正方形的性质得到S△BOC=$\frac{1}{4}$S正方形ABCD于是得到结论;
(3)根据(1)的结论得到△OEF是等腰直角三角形,根据等腰直角三角形的性质得到∠OEK=45°当OE=OK,当KE=KO,当EO=EK,即可得到结论.
解答 (1)证明:∵四边形ABCD是正方形,
∴OB=OC∠BOC=90°,
∠OBE=∠OCF=45°,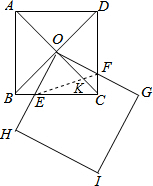
∵四边形OHIG是正方形,
∴∠GOH=90°,
∴∠EOC+∠COF=90°,
∵∠EOC+∠BOE=90°,
∴∠BOE=∠COF,
在△BOE和△COF中∠$\left\{\begin{array}{l}∠OBE=∠OCF\\ OB=OC\\∠BOE=∠COF\end{array}\right.$,
∴△BOE≌△COF(ASA),
∴BE=CF;
(2)四边形OECF的面积没有变化,
由(1)得:△BOE≌△COF
∴S四边形OECF=S△OEC+S△COF=S△OEC+S△BOE=S△BOC,
易知:S△BOC=$\frac{1}{4}$S正方形ABCD,
∵S四边形ABCD=22=4,
∴S△BOC=$\frac{1}{4}$S△BOC=$\frac{1}{4}$×4=1,
即:四边形OECF的面积没有变化;
(3)连接EF交AC于K,
由(1)得:∠EOK=∠DOF,OE=OF,
又∠GOH=90°,即△OEF是等腰直角三角形,
∴∠OEK=45°,
当OE=OK,显然不成立;
当KE=KO,即∠KEO=∠EOK=∠DOF=45°,
当EO=EK,即∠DOF=∠EOK=$\frac{180°-45°}{2}$=67.5°,
故当△OEK是等腰三角形时,∠DOF的度数是45°或67.5°.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质和判定,正方形的性质,证得BE=CF是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com