
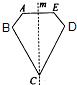
 16、如图,如果直线m是多边形ABCDE的对称轴,其中∠A=130°,∠B=110°.那么∠BCD的度数等于
16、如图,如果直线m是多边形ABCDE的对称轴,其中∠A=130°,∠B=110°.那么∠BCD的度数等于科目:初中数学 来源: 题型:
 如图,l1与l2是同一平面内的两条相交直线,它们有一个交点.如果在这个平面内,再画第三条直线l3,那么这三条直线最多可有
如图,l1与l2是同一平面内的两条相交直线,它们有一个交点.如果在这个平面内,再画第三条直线l3,那么这三条直线最多可有查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:中考必备’04全国中考试题集锦·数学 题型:044
先阅读下面的材料,然后解答问题:
在一条直线上有依次排列的n(n>1)台机床在工作,我们要设置一个零件供应站P,使这n台机床到供应站P的距离总和最小,要解决这个问题,先“退”到比较简单的情形:
如图①,如果直线上有2台机床时,很明显设在A1和A2之间的任何地方都行,因为甲和乙所走的距离之和等于A1到A2的距离.
如图②,如果直线上有3台机床时,不难判断,供应站设在中间一台机床A2处最合适.因为如果P放在A2处,甲和丙所走的距离之和恰好为A1到A3的距离.而如果把P放在别处,例如D处,那么甲和丙所走的距离之和仍是A1到A3的距离,可是乙还得走从A2到D的这一段,这是多出来的.因此P放在A2处是最佳选择.
不难知道,如果直线上有4台机床,P应设在第2台与第3台之间的任何地方;有5台机床.P应设在第3台位置.

问题(1):有n台机床时,P应设在何处?
问题(2):根据问题(1)的结论,求|x-1|+|x-2|+|x-3|+…+|x-617|的最小值.
查看答案和解析>>
科目:初中数学 来源:2003年河北省中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com