
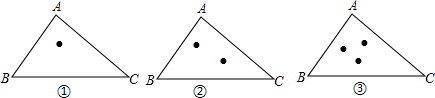
 (1)如图是小刚(A)、小明(B)、小勇(C)和他们各自影子的俯视图,他们所构成三角形地形的内部有一盏路灯,你认为如图是在白天阳光下的俯视图还是在晚上这盏路灯下的俯视图?
(1)如图是小刚(A)、小明(B)、小勇(C)和他们各自影子的俯视图,他们所构成三角形地形的内部有一盏路灯,你认为如图是在白天阳光下的俯视图还是在晚上这盏路灯下的俯视图? 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,沿同一条道路匀速行驶.设行驶时间为t(h),两车之间的距离为s(km),图中折线A-B-C-D表示s与t之间的函数关系.
一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,沿同一条道路匀速行驶.设行驶时间为t(h),两车之间的距离为s(km),图中折线A-B-C-D表示s与t之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
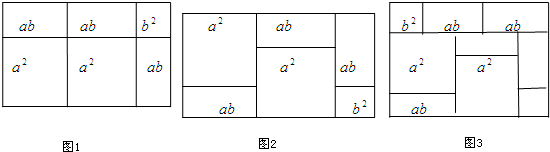
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | 3000 | 3050 | 3100 | 3150 | 3200 | 3250 | 3300 |
| y | 100 | 99 | 98 | 97 | 96 | 95 | 94 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com