
【题目】当今社会人们越来越离不开网络,电脑、手机被普遍使用,与此同时人们的视力也大大受到影响,2019年初某企业以25万元购得某项护目镜生产技术后,再投人100万元购买生产设备,进行该护目镜的生产加工,已知生产这种护目镜的成本价为每件20元,经过市场调研发现该产品的销售单价定在![]() 元比较合理,并且该产品的年销售量
元比较合理,并且该产品的年销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的函数关系式为
(元)之间的函数关系式为![]() .(年获利=年销售收入-生产成本-投资成本)
.(年获利=年销售收入-生产成本-投资成本)
(1)求该公司第一年的年获利![]() (万元)与销售单价
(万元)与销售单价![]() (元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?
(元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?
(2)2020年初我国爆发新冠肺炎,该公司决定向红十字会捐款20万元,另外每销售一件产品,就抽出1元钱作为捐款,若除去第一年的最大盈利(或最小亏损)以及第二年的捐款后,到2020年底,两年的总盈利不低于57.5万元,请你确定此时销售单价的范围.
【答案】(1)投资的第一年公司亏损,最少亏损12.5万元;(2)当两年的总盈利不低于57.5万元时,销售单价的范围为![]() .
.
【解析】
(1)分两种情况,根据一件利润乘以件数求出利润W,求出最大值进行比较即可得到答案;
(2)设两年的总盈利为![]() 万元,分两种情况:当
万元,分两种情况:当![]() 时,求出
时,求出![]() ,根据盈利不低于57.5万元,得到
,根据盈利不低于57.5万元,得到![]() ;当
;当![]() 时,求出
时,求出![]() ,根据
,根据![]() ,得到
,得到![]() ,将两种情况综合得到答案.
,将两种情况综合得到答案.
(1)当![]() ,
,![]() =
=![]() ,
,
∴![]() 时,
时,![]() .
.
当![]() 时,
时,
![]() =
=![]() ,
,
∴![]() 时,
时,![]() .
.
![]() ,
,
∴投资的第一年公司亏损,最少亏损12.5万元.
(2)设两年的总盈利为![]() 万元.
万元.
当![]() 时,
时,
![]() .
.
∵盈利不低于57.5万元,
![]() .
.
![]() .
.
又![]() ,
,
∴此时,两年总盈利不低于57.5万元时,![]() ;
;
当![]() 时,
时,![]()
![]()
∵盈利不低于57.5万元,
![]()
![]() .
.
又![]() ,
,
∴![]() .
.
综上,当两年的总盈利不低于57.5万元时,![]() .
.


科目:初中数学 来源: 题型:
【题目】在中俄“海上联合—2014”反潜演习中,我军舰A测得潜艇C的俯角为300.位于军舰A正上方1000米的反潜直升机B侧得潜艇C的俯角为680,试根据以上数据求出潜艇C离开海平面的下潜深度。(结果保留整数。参考数据:sin680≈0.9,cos680≈0.4,,tan680≈2.5. ![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品![]() 千克.
千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用![]() (元)与
(元)与![]() (千克)之间的函数关系式;
(千克)之间的函数关系式;
(2)若小明快递的物品超过1千克,则他应选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“南昌之星”摩天轮,位于江西省南昌市红谷滩新区红角洲赣江边上的赣江市民公园,摩天轮高![]() (最高点到地面的距离).如图,点
(最高点到地面的距离).如图,点![]() 是摩天轮的圆心,
是摩天轮的圆心,![]() 是其垂直于地面的直径,小贤在地面点
是其垂直于地面的直径,小贤在地面点![]() 处利用测角仪测得摩天轮的最高点
处利用测角仪测得摩天轮的最高点![]() 的仰角为
的仰角为![]() ,测得圆心
,测得圆心![]() 的仰角为
的仰角为![]() ,则摩天轮的半径为________
,则摩天轮的半径为________![]() (结果保留
(结果保留![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() =
=![]() (
(![]() 为任意实数)
为任意实数)
(1)无论![]() 取何值,抛物线
取何值,抛物线![]() 恒过两点________,________.
恒过两点________,________.
(2)当![]() 时,设抛物线
时,设抛物线![]() 在第一象限依次经过整数点(横、纵坐标均为整数的点)为
在第一象限依次经过整数点(横、纵坐标均为整数的点)为![]() ,
,![]() …
…![]() .将抛物线
.将抛物线![]() 沿直线
沿直线![]()
![]() 平移,平移后的抛物线记为
平移,平移后的抛物线记为![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() 的顶点为
的顶点为![]() (
(![]() ,例如
,例如![]() 时,抛物线
时,抛物线![]() 经过点
经过点![]() ,
,![]() 顶点为
顶点为![]() )
)
①抛物线![]() 的解析式为________;顶点坐标为________;
的解析式为________;顶点坐标为________;
②在抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标,并判断四边形
的坐标,并判断四边形![]() 的形状;若不存在,请说明理由.
的形状;若不存在,请说明理由.
③直接写出线段![]() 的长________.
的长________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教育主管部门针对中小学生非统考学科的教学情况进行年终考评,抽取某校八年级部分同学的成绩作为样本,把成绩按![]() (优秀)、
(优秀)、![]() (良好)、
(良好)、![]() (及格)、
(及格)、![]() (不及格)四个级别进行统计,并绘成如图所示不完整的条形统计图和扇形统计图.
(不及格)四个级别进行统计,并绘成如图所示不完整的条形统计图和扇形统计图.
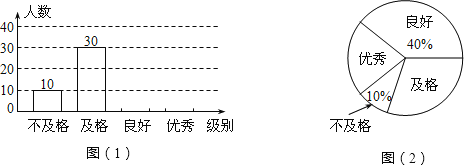
(1)求被抽取的学生人数;
(2)补全条形统计图,并求![]() 的圆心角度数;
的圆心角度数;
(3)该校八年级有![]() 名学生,请估计达到
名学生,请估计达到![]() 、
、![]() 两级的总人数.
两级的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年4月,过敏体质检测中心等机构开展了青少年形体测评,专家组随机抽查了某市若干名初中生坐姿、站姿、走姿的好坏情况.我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制成了如下两幅不完整的统计图,请你根据图中所给信息解答些列问题:
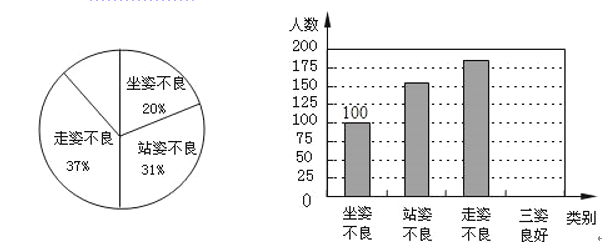
(1)请将两幅图补充完整;
(2)如果全市有10万名初中生,那么全市初中生中,三姿良好的学生约有 人.
(3)根据统计结果,请你简单谈谈自己的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),△ABO绕点B顺时针旋转,得△A′BO′,点A、O旋转后的对应点为A′、O′,记旋转角为α.
(1)如图1,若α=90°,求AA′的长;
(2)在(1)的条件下,边OA上的一点M旋转后的对应点为N,当O′M+BN取得最小值时,在图中画出求点M的位置,并求出点N的坐标。
(3)如图2,在△ABO绕点B顺时针旋转过程中,以AB、A′B为邻边画菱形AB A′E,F是AB的中点,连A′F交BE于P,BP的垂直平分线交AB于K,当α从60°到90°的变化过程中,点K的位置是否变化?若不变,求BK的长并直接写出此变化过程中点P的运动路径长.
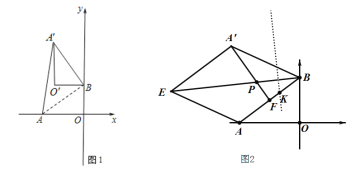
查看答案和解析>>
科目:初中数学 来源: 题型:
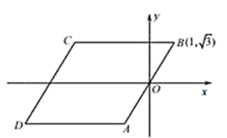
【题目】如图,已知四边形ABCD是菱形,BC∥x轴,点B的坐标是(1,![]() ),坐标原点O是AB的中点.动圆⊙P的半径是
),坐标原点O是AB的中点.动圆⊙P的半径是![]() ,圆心在x轴上移动,若⊙P在运动过程中只与菱形ABCD的一边相切,则点P的横坐标m 的取值范围是_________.
,圆心在x轴上移动,若⊙P在运动过程中只与菱形ABCD的一边相切,则点P的横坐标m 的取值范围是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com