
【题目】如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM.下列结论:①DF=DN ②AE=CN;③△DMN是等腰三角形;④∠BMD=45°,其中正确的结论个数是 ( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】试题分析:求出BD=AD,∠DBF=∠DAN,∠BDF=∠ADN,证△DFB≌△DAN,即可判断①,证△ABF≌△CAN,推出CN=AF=AE,即可判断②;根据A、B、D、M四点共圆求出∠ADM=22.5°,即可判断④,根据三角形外角性质求出∠DNM,求出∠MDN=∠DNM,即可判断③.
解:∵∠BAC=90°,AC=AB,AD⊥BC,
∴∠ABC=∠C=45°,AD=BD=CD,∠ADN=∠ADB=90°,
∴∠BAD=45°=∠CAD,
∵BE平分∠ABC,
∴∠ABE=∠CBE=![]() ∠ABC=22.5°,
∠ABC=22.5°,
∴∠BFD=∠AEB=90°﹣22.5°=67.5°,
∴∠AFE=∠BFD=∠AEB=67.5°,
∴AF=AE,
∵M为EF的中点,
∴AM⊥BE,
∴∠AMF=∠AME=90°,
∴∠DAN=90°﹣67.5°=22.5°=∠MBN,
在△FBD和△NAD中

∴△FBD≌△NAD,
∴DF=DN,∴①正确;
在△AFB和△△CNA中

∴△AFB≌△CAN,
∴AF=CN,
∵AF=AE,
∴AE=CN,∴②正确;
∵∠ADB=∠AMB=90°,
∴A、B、D、M四点共圆,
∴∠ABM=∠ADM=22.5°,
∴∠DMN=∠DAN+∠ADM=22.5°+22.5°=45°,∴④正确;
∵∠DNA=∠C+∠CAN=45°+22.5°=67.5°,
∴∠MDN=180°﹣45°﹣67.5°=67.5°=∠DNM,
∴DM=MN,∴△DMN是等腰三角形,∴③正确;
即正确的有4个,
故选D.



 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
【题目】某码头上有20名工人装载一批货物,已知每人往一艘轮船上装载2吨货物,装载完毕恰好用了6天,轮船到达目的地后,另一批工人开始卸货,计划平均每天卸货v吨,刚要卸货时遇到紧急情况,要求船上的货物卸载完毕不超过4天,则这批工人实际每天至少应卸货( )
A.30吨
B.40吨
C.50吨
D.60吨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪灵感.他惊喜地发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连接DB,过点D作BC边上的高DF,则DF=EC=b-a.
∵S四边形ADCB=S△ACD+S△ABC=![]() b2+
b2+![]() ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB=![]() c2+
c2+![]() a(b-a),
a(b-a),
∴![]() b2+
b2+![]() ab=
ab=![]() c2+
c2+![]() a(b-a),
a(b-a),
∴a2+b2=c2.
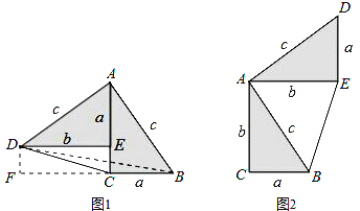
请参照上述证法,利用图2完成下面的证明:
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.
求证:a2+b2=c2.
证明:连接 ,
∵S五边形ACBED= ,
又∵S五边形ACBED= ,
∴ ,
∴a2+b2=c2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断中错误的是( )
A. 有两角和其中一个角的对边对应相等的两个三角形全等
B. 有一边相等的两个等边三角形全等
C. 有两边和一角对应相等的两个三角形全等
D. 有两边和其中一边上的中线对应相等的两个三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
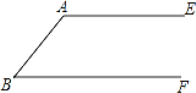
【题目】如图,AE∥BF,先按(1)的要求作图,再按(2)的要求证明
(1)用直尺和圆规作出∠ABF的平分线BD交AE于点D,再作出BD的中点O(不写作法,保留作图痕迹)
(2)连接(1)所作图中的AO并延长与BF相交于点C,连接DC,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AD是∠BAC的平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确的个数有( )

A.3个 B.2个 C.1个 D.0个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com