
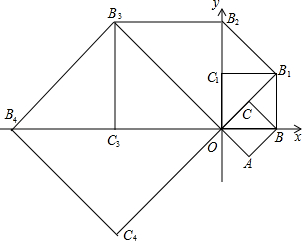
 如图,在平面直角坐标系xOy中,有一边为1的正方形OABC,点B在x轴的正半轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则B2的坐标是(0,2$\sqrt{2}$);B2015的坐标是(${2}^{254}\sqrt{2}$,-${2}^{254}\sqrt{2}$).
如图,在平面直角坐标系xOy中,有一边为1的正方形OABC,点B在x轴的正半轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则B2的坐标是(0,2$\sqrt{2}$);B2015的坐标是(${2}^{254}\sqrt{2}$,-${2}^{254}\sqrt{2}$). 分析 根据正方形的性质找出部分Bn点的坐标,根据坐标的变化找出变化规律“B8n(24n$\sqrt{2}$,0),B8n+1(24n$\sqrt{2}$,24n$\sqrt{2}$),B8n+2(0,24n+1$\sqrt{2}$),B8n+3(-24n+1$\sqrt{2}$,24n+1$\sqrt{2}$),B8n+4(-24n+2$\sqrt{2}$,0),B8n+5(-24n+2$\sqrt{2}$,-24n+2$\sqrt{2}$),B8n+6(0,-24n+3$\sqrt{2}$),B8n+7(24n+3$\sqrt{2}$,-24n+3$\sqrt{2}$),(n为自然数)”,依次规律即可得出结论.
解答 解:观察,发现规律:B($\sqrt{2}$,0),B1($\sqrt{2}$,$\sqrt{2}$),B2(0,2$\sqrt{2}$),B3(-2$\sqrt{2}$,2$\sqrt{2}$),B4(-4$\sqrt{2}$,0),B5(-4$\sqrt{2}$,-4$\sqrt{2}$),B6(0,-8$\sqrt{2}$),B7(8$\sqrt{2}$,-8$\sqrt{2}$),B8(16$\sqrt{2}$,0),…,
∴B8n(24n$\sqrt{2}$,0),B8n+1(24n$\sqrt{2}$,24n$\sqrt{2}$),B8n+2(0,24n+1$\sqrt{2}$),B8n+3(-24n+1$\sqrt{2}$,24n+1$\sqrt{2}$),B8n+4(-24n+2$\sqrt{2}$,0),B8n+5(-24n+2$\sqrt{2}$,-24n+2$\sqrt{2}$),B8n+6(0,-24n+3$\sqrt{2}$),B8n+7(24n+3$\sqrt{2}$,-24n+3$\sqrt{2}$),(n为自然数).
∵2015=251×8+7,
∴B2015的坐标为(${2}^{254}\sqrt{2}$,-${2}^{254}\sqrt{2}$).
故答案为:(0,2$\sqrt{2}$);(${2}^{254}\sqrt{2}$,-${2}^{254}\sqrt{2}$).
点评 本题考查了规律型中坐标的变化类,解题的关键是找出坐标的变化规律.本题属于基础题,难度不大,解决该题型题目时,根据坐标的变化找出变化规律是关键.


科目:初中数学 来源: 题型:选择题
| A. | 测量对角线是否相互垂直 | B. | 测量两组对边是否分别相等 | ||
| C. | 测量对角线是否相等 | D. | 测量其中三个角是否都为直角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com