
 如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )| A. | $\frac{2π}{3}$-$\sqrt{3}$ | B. | $\frac{2π}{3}$-$\frac{\sqrt{3}}{2}$ | C. | π-$\frac{\sqrt{3}}{2}$ | D. | π-$\sqrt{3}$ |
分析 根据菱形的性质得出△DAB是等边三角形,进而利用全等三角形的判定得出△ABG≌△DBH,得出四边形GBHD的面积等于△ABD的面积,进而求出即可.
解答 解:连接BD,
∵四边形ABCD是菱形,∠A=60°,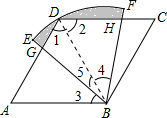
∴∠ADC=120°,
∴∠1=∠2=60°,
∴△DAB是等边三角形,
∵AB=2,
∴△ABD的高为$\sqrt{3}$,
∵扇形BEF的半径为2,圆心角为60°,
∴∠4+∠5=60°,∠3+∠5=60°,
∴∠3=∠4,
设AD、BE相交于点G,设BF、DC相交于点H,
在△ABG和△DBH中,
$\left\{\begin{array}{l}{∠A=∠2}\\{AB=BD}\\{∠3=∠4}\end{array}\right.$,
∴△ABG≌△DBH(ASA),
∴四边形GBHD的面积等于△ABD的面积,
∴图中阴影部分的面积是:S扇形EBF-S△ABD=$\frac{60π×{2}^{2}}{360}$-$\frac{1}{2}$×2×$\sqrt{3}$=$\frac{2π}{3}$-$\sqrt{3}$.
故选:A.
点评 此题主要考查了扇形的面积计算以及全等三角形的判定与性质等知识,根据已知得出四边形EBFD的面积等于△ABD的面积是解题关键.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | 购买一张福利彩票中奖了 | |
| B. | 通常水加热到100℃时会沸腾 | |
| C. | 在地球上,抛出的篮球会下落 | |
| D. | 掷一枚骰子,向上一面的字数一定大于零 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| (1)(-2)+(-7); | (2)-32-5; | (3)(-30.5)×0.2; |
| (4)12-(-18)+(-7)-15; | (5)(-$\frac{3}{4}$)×(-1$\frac{1}{2}$)×0÷(-2$\frac{1}{4}$); | (6)-9×(-11)÷3÷(-3); |
| (7)-18÷2$\frac{1}{4}$-$\frac{4}{9}$÷(-$\frac{2}{3}$); | (8)($\frac{9}{10}$-$\frac{2}{15}$+$\frac{1}{6}$)×30; | (9)1-3.9÷[1-$\frac{3}{4}$-(-0.5)]. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 国庆节即将来临,张华高兴地看着某月的日历,发现其中有很有趣的问题,他用笔在上面画如图所示的十字框,若设任意一个十字框里的五个数为a、b、c、d、k.设中间的一个数为k,如图:试回答下列问题:
国庆节即将来临,张华高兴地看着某月的日历,发现其中有很有趣的问题,他用笔在上面画如图所示的十字框,若设任意一个十字框里的五个数为a、b、c、d、k.设中间的一个数为k,如图:试回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com