
����Ŀ����֪b����С������������a��c����|a+1|+��c+6��2=0��
��1����գ�a=������b=������c=������
��2��a��b��c������������Ӧ�ĵ�ֱ�ΪA��B��C��P�������ϵ�A��B֮��һ���㣨�����A��B�غϣ������Ӧ����Ϊx��|x+1|+|x��1|= ��
��3���ڣ�1������2���������£���A��B��C��ʼ��������ͬʱ�˶�������C�͵�A�ֱ���ÿ��6����λ���Ⱥ�2����λ���ȵ��ٶ������˶�����B��ÿ��2����λ���ȵ��ٶ������˶�������t���ӹ�������A���C֮��ľ����ʾΪAC����A��B֮��ľ����ʾΪAB�����ʣ�AC��AB��ֵ�Ƿ�����ʱ��t�ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ.

���𰸡���1��-1��1��-6 ��2��2 ��3�����䣻3
��������
��1��������С����������1���Ƴ�b=1�������÷Ǹ������������a��c���ɣ�
��2������ȷ��x�ķ�Χ���ٻ������ֵ���ɣ�
��3��AC��AB��ֵ���䣮����������t��ʾ��AC��AB���ɽ�����⣮
�⣺��1����b����С����������
��b=1��
��|a+1|+��c+6��2=0��a+1=0��c+6=0��
��a=-1�� b=1��c=-6��
�ʴ�Ϊ��-1��1��-6��
��2��������-1��x��1��
��|x+1|+|x��1|=x+1-��x-1��= x+1-x+1=2��
��3�����䣬������AC=��-1-2t��-��-6-6t��=5+4t��AB=��1+2t��-��-1-2t��=2+4t��
��AC-AB=��5+4t��-��2+4t��=3��
��AC-AB��ֵ���䣬AC-AB=3��
�ʴ�Ϊ����1��-1��1��-6 ��2��2 ��3�����䣻3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼʾ������С�����������Σ���15������������Ҫ��__________����С������n������������Ҫ��__________����С��.
![]()
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������κ���y1��y2��ͼ��Ķ���ֱ�Ϊ��a��b������c��d������a=��c��b=2d���ҿ��ڷ�����ͬʱ�����y1��y2�������������κ�������
��1����д�����κ���y=x2+x+1��һ�������������κ�������
��2����֪����x�Ķ��κ���y1=x2+nx�Ͷ��κ���y2=nx2+x������y1+y2ǡ��y1��y2�������������κ���������n��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
(1)![]() (2)
(2)![]()
(3)��54��![]() ��
��![]() ��
��![]() (4)
(4)![]()
(5)��5��![]() +����9����
+����9����![]() +17��
+17��![]() (6)
(6)![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
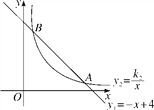
����Ŀ����ͼ������y1����x��4��ͼ���뺯��y2��![]() (x��0)��ͼ����A(a��1)��B(1��b)���㣮
(x��0)��ͼ����A(a��1)��B(1��b)���㣮
(1)����y2�ı���ʽ��
(2)�۲�ͼ�Ƚϵ�x��0ʱ��y1��y2�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ����
����![]() �ش�;�绰����ʱ�շѣ�3�������շ�2.7Ԫ��3���Ӻ�ÿͨ��1�����շ�1.2Ԫ��ij����
�ش�;�绰����ʱ�շѣ�3�������շ�2.7Ԫ��3���Ӻ�ÿͨ��1�����շ�1.2Ԫ��ij����![]() ����
����![]() �ش�绰������
�ش�绰������![]() ����
����![]() Ϊ����)���ӣ�����Ϊ
Ϊ����)���ӣ�����Ϊ![]() Ԫ��
Ԫ��
(1)�![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
(2)��ͨ��5���ӣ�����Ҫ���Ѷ���Ԫ?
(3)��ij��ͨ������Ϊ8.7Ԫ������ͨ�����ٷ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ����(����)
�ٵ������������߳�Ϊ2��5���������ܳ���9��12������������![]() �ڣ�2�ͣ�1֮�䣻�������ε��ڽǺ�����Ǻ͵�2��������a��b����a��b��0.�����������Ǽ����⣻�ݱ�ƫ��30������ƫ��50��������������ɵĽ�Ϊ80��.
�ڣ�2�ͣ�1֮�䣻�������ε��ڽǺ�����Ǻ͵�2��������a��b����a��b��0.�����������Ǽ����⣻�ݱ�ƫ��30������ƫ��50��������������ɵĽ�Ϊ80��.
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������У���ABC�Ķ�����ڸ���ϣ�����������ֱ������ϵ�н���������⣺
��1��������ABC����ԭ��O�����ĶԳƵ���A1B1C1��
��2��ֱ��д������A��B��CΪ�����ƽ���ı��εĵ��ĸ�����D�������� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
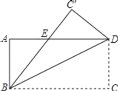
����Ŀ����ͼ������ABCD����ֱ��BD�۵���ʹ��C����C������BC����AD�ڵ�E��AD=4��AB=3����AE�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com