
【题目】已知,如图,一次函数![]() 与x轴、y轴分别交于点A和点B,A点坐标为(3,0),∠OAB=45°.
与x轴、y轴分别交于点A和点B,A点坐标为(3,0),∠OAB=45°.

(1)求一次函数的表达式;
(2)点P是x轴正半轴上一点,以P为直角顶点,BP为腰在第一象限内作等腰Rt△BPC,连接CA并延长交y轴于点Q.
①若点P的坐标为(4,0),求点C的坐标,并求出直线AC的函数表达式;
②当P点在x轴正半轴运动时,Q点的位置是否发现变化?若不变,请求出它的坐标;如果变化,请求出它的变化范围.
【答案】(1)![]() ;(2)①点C(7,4);
;(2)①点C(7,4);![]() ;②点Q的位置不发生变化,点Q的坐标为(0,-3).
;②点Q的位置不发生变化,点Q的坐标为(0,-3).
【解析】
试题(1)由∠AOB=90°,∠OAB=45°,可得∠OBA=∠OAB=45°,即OA=OB,由A(3,0),可得B(0,3),代入y=kx+b可得出k,b的值,即可得出一次函数的表达式;
(2)①过点C作x轴的垂线,垂足为D,易证△BOP≌△PDC,进而得出点P,C的坐标,把点A,C的坐标代入y=k1x+b1求解即可;
②由△BOP≌△PDC,可得PD=BO,CD=PO,由线段关系进而得出OA=OB,得出AD=CD,由角的关系可得△AOQ是等腰直角三角形,可得出OQ=OA,即可得出点Q的坐标.
试题解析:解:(1)∵∠AOB=90°,∠OAB=45°,
∴∠OBA=∠OAB=45°,
∴OA=OB,
∵A(3,0),
∴B(0,3),
∴![]() ,解得
,解得![]() ,
,
∴![]() ;
;
(2)①过点C作x轴的垂线,垂足为D,
∵∠BPO+∠CPD=∠PCD+∠CPD=90°,
∴∠BPO=∠PCD,
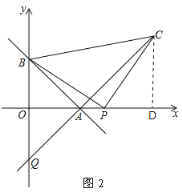
在△BOP和 △PDC 中,
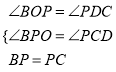 ,
,
∴ △BOP≌ △PDC(AAS).
∴PD=BO=3,CD=PO,
∵P(4,0),
∴CD="PO=4," 则OD=3+4=7,
∴ 点C(7,4),
设直线AC的函数关系式为![]() ,
,
则![]() ,解得
,解得![]() ,
,
∴直线AC的函数关系式为![]() ;
;
②点Q的位置不发生变化.
理由:由①知 △BOP≌ △PDC,
当P点在x轴正半轴运动时,仍有△BOP≌ △PDC,
∴PD=BO,CD=PO,
∴PO+PD=CD+OB,
即OA+AD=OB+CD,
又∵OA=OB,
∴AD=CD,
∴∠CAD=45°,
∴∠CAD=∠QAO=45°,
∴OQ=OA=3,
即点Q的坐标为(0,-3).


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为S2,△B3C2B4的面积为S3,如此下去,则Sn=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BD⊥AC于点D,AD=3.5cm,点P、Q分别为AB、AD上的两个定点且BP=AQ=2cm,若在BD上有一动点E使PE+QE最短,则PE+QE的最小值为_____cm

查看答案和解析>>
科目:初中数学 来源: 题型:
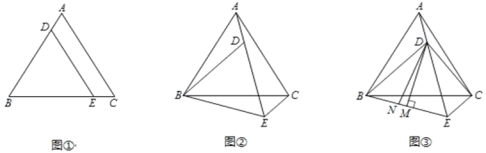
【题目】已知:如图①,△ABC是等边三角形,点D、E分别在边AB、BC上,且BD=BE,连接DE.
(1)求证:DE∥AC;
(2)将图①中的△BDE绕点B顺时针旋转,使得点A、D、E在同一条直线上,如图②,求∠AEC的度数;
(3)在(2)的条件下,如图③,连接CD,过点D作DM⊥BE于点M,在线段BM上取点N,使得∠DNE+∠DCE=180°.请探索三条线段EN,MN,EC之间的关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1(0,1),A2(![]() ,
,![]() ),A3(
),A3(![]() ,
,![]() ),A4(0,2),A5(
),A4(0,2),A5(![]() ,
,![]() ),A6(
),A6(![]() ,
,![]() ),A7(0,3),A8(
),A7(0,3),A8(![]() ,
,![]() ),A9(
),A9(![]() ,
,![]() ),…,则点A2010的坐标是______.
),…,则点A2010的坐标是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三位歌手进入“我是歌手”的决赛,他们通过抽签来决定演唱顺序.
(1)求甲第一位出场的概率;
(2)求甲比乙先出场的概率,请用列表或画树状图的方法进行分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
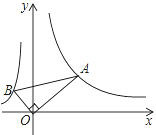
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=![]() (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )
A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A点的坐标为(m,3),AB⊥x轴于点B,tan∠OAB=![]() ,反比例函数y1=
,反比例函数y1=![]() 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.
(1)求反比例函数解析式;
(2)设直线OA的解析式为y2=nx,请直接写出y1<y2时,自变量x的取值范围 .
(3)如图2,若函数y=3x与y1=![]() 的图象的另一支交于点M,求△OMB与四边形OCDB的面积的比值.
的图象的另一支交于点M,求△OMB与四边形OCDB的面积的比值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1 A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2 A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为 ;第n个三角形中以An为顶点的内角的度数为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com