
【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:
PA= , PC=;
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后,P,Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由. 
【答案】
(1)t;34﹣t
(2)解:当P点在Q点右侧,且Q点还没有追上P点时,
3t+2=14+t
解得:t=6,
∴此时点P表示的数为﹣4,
当P点在Q点左侧,且Q点追上P点后,相距2个单位,
3t﹣2=14+t解得:t=8,
∴此时点P表示的数为﹣2,
当Q点到达C点后,当P点在Q点左侧时,
14+t+2+3t﹣34=34
解得:t=13,
∴此时点P表示的数为3,
当Q点到达C点后,当P点在Q点右侧时,
14+t﹣2+3t﹣34=34
解得:t=14,
∴此时点P表示的数为4,
综上所述:点P表示的数为﹣4,﹣2,3,4
【解析】解:(1)∵动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒,
∴P到点A的距离为:PA=t,P到点C的距离为:PC=(24+10)﹣t=34﹣t;
所以答案是:t,34﹣t;
【考点精析】掌握数轴和两点间的距离是解答本题的根本,需要知道数轴是规定了原点、正方向、单位长度的一条直线;同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.


科目:初中数学 来源: 题型:
【题目】小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表
抛掷次数 | 100 | 200 | 300 | 400 | 500 |
正面朝上的频数 | 53 | 98 | 156 | 202 | 249 |
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
A.200B.300C.400D.500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年以来,“新型冠状肺炎”流行,这种病毒的直径大约为150纳米,1纳米=0.000000001米=10-9米,把150纳米用科学记数法表示正确的是( )
A.1.5×10-2米B.1.5×10-7米C.1.5×10-9米D.1.5×10-11米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国地大物博,过去由于交通不便,一些地区的经济发展受到了制约,自从“高铁网络”在全国陆续延伸以后,许多地区的经济和旅游发生了翻天覆地的变化,高铁列车也成为人们外出旅行的重要交通工具.李老师从北京到某地去旅游,从北京到该地普快列车行驶的路程约为1 352 km,高铁列车比普快列车行驶的路程少52 km,高铁列车比普快列车行驶的时间少8 h.已知高铁列车的平均时速是普快列车平均时速的2.5倍,求高铁列车的平均时速.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,当平行四边形CBPQ的面积为30时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
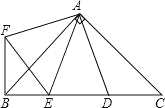
【题目】如图,在Rt△ABC中,AB=AC,D,E是斜边上BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
①BF⊥BC;②△AED≌△AEF;③BE+DC=DE;④BE2+DC2=DE2
其中正确的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com