
 如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为65和33,则△EDF的面积为16.
如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为65和33,则△EDF的面积为16. 分析 作DH⊥AC于H,根据角平分线的性质得到DF=DH,证明Rt△FDE≌Rt△HDG和Rt△FDA和Rt△HDA,根据题意列方程,解方程即可.
解答 解: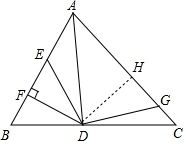 作DH⊥AC于H,
作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,
∴DF=DH,
在Rt△FDE和Rt△HDG中,
$\left\{\begin{array}{l}{DF=DH}\\{DE=DG}\end{array}\right.$,
∴Rt△FDE≌Rt△HDG,
同理,Rt△FDA和Rt△HDA,
设△EDF的面积为x,
由题意得,65-x=33+x,
解得,x=16,即△EDF的面积为16,
故答案为:16.
点评 本题考查的是角平分线的性质、全等三角形的判定和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:填空题
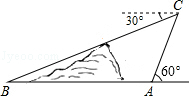 如图,在小山的东侧A点处有一个热气球,由于受西风的影响,以每分钟30米的速度沿与地面成60°角的方向飞行,20分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则A、B两点间的距离为600米.
如图,在小山的东侧A点处有一个热气球,由于受西风的影响,以每分钟30米的速度沿与地面成60°角的方向飞行,20分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则A、B两点间的距离为600米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 建筑工人砌墙时拉的参照线是运用“两点之间线段最短”的原理 | |
| B. | 修理损坏的椅子腿时斜钉的木条是运用“三角形稳定性”的原理 | |
| C. | 测量跳远的成绩是运用“垂线段最短”的原理 | |
| D. | 将车轮设计为圆形是运用了“圆的旋转对称性”原理 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
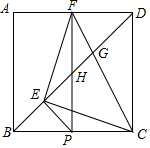 如图,正方形ABCD中,P为BC上一点,PE⊥BD于E,PF⊥AD于F,连接EF、CF.
如图,正方形ABCD中,P为BC上一点,PE⊥BD于E,PF⊥AD于F,连接EF、CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
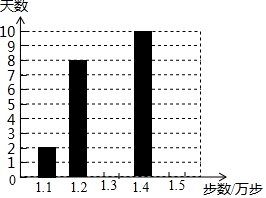 乐乐是一名健步运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
乐乐是一名健步运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com